题目内容
14.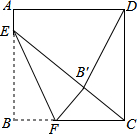 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$.
分析 根据翻折的性质,可得B′E的长,根据勾股定理,可得CE的长,根据等腰三角形的判定,可得答案.
解答 解:(i)当B′D=B′C时,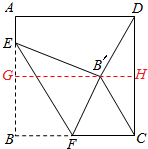
过B′点作GH∥AD,则∠B′GE=90°,
当B′C=B′D时,AG=DH=$\frac{1}{2}$DC=8,
由AE=3,AB=16,得BE=13.
由翻折的性质,得B′E=BE=13.
∴EG=AG-AE=8-3=5,
∴B′G=$\sqrt{B′{E}^{2}-E{G}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴B′H=GH-B′G=16-12=4,
∴DB′=$\sqrt{B′{H}^{2}+D{H}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$
(ii)当DB′=CD时,则DB′=16(易知点F在BC上且不与点C、B重合).
(iii)当CB′=CD时,
∵EB=EB′,CB=CB′,
∴点E、C在BB′的垂直平分线上,
∴EC垂直平分BB′,
由折叠可知点F与点C重合,不符合题意,舍去.
综上所述,DB′的长为16或4$\sqrt{5}$.
故答案为:16或4$\sqrt{5}$.
点评 本题考查了翻折变换,利用了翻折的性质,勾股定理,等腰三角形的判定.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目


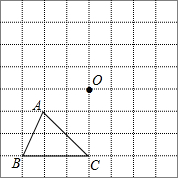 如图,在方格网中已知格点△ABC和点O.
如图,在方格网中已知格点△ABC和点O.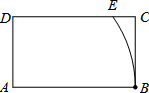 如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则$\widehat{BE}$的长度为$\frac{2}{3}π$.
如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则$\widehat{BE}$的长度为$\frac{2}{3}π$. 如图,点A(3,5)关于原点O的对称点为点C,分别过点A,C作y轴的平行线,与反比例函数y=$\frac{k}{x}$(0<k<15)的图象交于点B,D,连接AD,BC,AD与x轴交于点E(-2,0).
如图,点A(3,5)关于原点O的对称点为点C,分别过点A,C作y轴的平行线,与反比例函数y=$\frac{k}{x}$(0<k<15)的图象交于点B,D,连接AD,BC,AD与x轴交于点E(-2,0).