题目内容
 如图,在△ABC中,∠BAC=110°,AB,AC的垂直平分线分别交BC于点D,E,则∠DAE=
如图,在△ABC中,∠BAC=110°,AB,AC的垂直平分线分别交BC于点D,E,则∠DAE=考点:线段垂直平分线的性质
专题:
分析:根据三角形内角和定理求出∠B+∠C=70°,根据线段垂直平分线性质得出AD=BD,AE=EC,推出∠1=∠B,∠2=∠C,推出∠1+∠2=70°,代入∠DAE=∠BAC-(∠1+∠2)求出即可.
解答:解:∵AB,AC的垂直平分线分别交BC于点D,E,
∴AD=BD,AE=EC,
∴∠1=∠B,∠2=∠C,
∵∠BAC=110°,
∴∠B+∠C=180°-110°=70°,
∴∠1+∠2=70°,
∴∠DAE=∠BAC-(∠1+∠2)=110°-70°=40°,
故答案为:40°.
∴AD=BD,AE=EC,
∴∠1=∠B,∠2=∠C,
∵∠BAC=110°,
∴∠B+∠C=180°-110°=70°,
∴∠1+∠2=70°,
∴∠DAE=∠BAC-(∠1+∠2)=110°-70°=40°,
故答案为:40°.
点评:本题考查了等腰三角形的性质,三角形内角和定理,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
一个等腰梯形的两底之差为12,高为6,则等腰梯形的两底的一个锐角为( )
| A、75° | B、60° |
| C、45° | D、30° |
已知|x-1|<2,则x的取值范围是( )
| A、x>3或x<-1 |
| B、x<3或x>-1 |
| C、-1<x<3 |
| D、-3<x<1 |
 如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图.那么构成这个立体图形的小正方体有( )
如图是由一些相同的小正方体构成的立体图形分别从正面、左面、上面看到的形状图.那么构成这个立体图形的小正方体有( )| A、4个 | B、5个 | C、6个 | D、7个 |
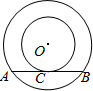 如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于C.设弦AB的长为d,圆环的面积S与d之间有怎样的数量关系?
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于C.设弦AB的长为d,圆环的面积S与d之间有怎样的数量关系? 如图,∠AOB=50°,OC是∠AOB的平分线,AC⊥OA于点A,BC⊥BO于点B,则∠BAC的度数是
如图,∠AOB=50°,OC是∠AOB的平分线,AC⊥OA于点A,BC⊥BO于点B,则∠BAC的度数是