Question

3．在平面直角坐标系xOy中，过⊙C上一点P作⊙C的切线l．当入射光线照射在点P处时，产生反射，且满足：反射光线与切线l的夹角和入射光线与切线l的夹角相等，点P称为反射点．规定：光线不能“穿过”⊙C，即当入射光线在⊙C外时，只在圆外进行反射；当入射光线在⊙C内时，只在圆内进行反射．特别地，圆的切线不能作为入射光线和反射光线．
光线在⊙C外反射的示意图如图1所示，其中∠1=∠2．
（1）自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示，P₁是第1个反射点．请在图2中作出光线经⊙C第二次反射后的反射光线；
（2）当⊙O的半径为1时，如图3，
①第一象限内的一条入射光线平行于x轴，且自⊙O的外部照射在其上点P处，此光线经⊙O反射后，反射光线与y轴平行，则反射光线与切线l的夹角为45°；
②自点A（-1，0）出发的入射光线，在⊙O内不断地反射．若第1个反射点P₁在第二象限，且第12个反射点P₁₂与点A重合，则第1个反射点P₁的坐标为（-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}）$；
（3）如图4，点M的坐标为（0，2），⊙M的半径为1．第一象限内自点O出发的入射光线经⊙M反射后，反射光线与坐标轴无公共点，求反射点P的纵坐标的取值范围．

Answer 1

分析 （1）（2）两个问题，要根据题意，画出图象，可以解决．
（3）当反射光线平行X轴时，反射光线与坐标轴没有交点，只要求出这样的反射点，就可以解决这个问题了．

解答 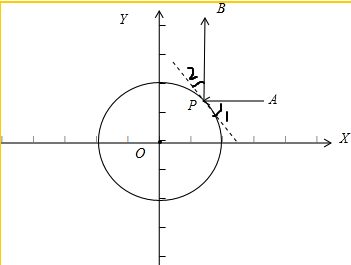解：（1）答案如图：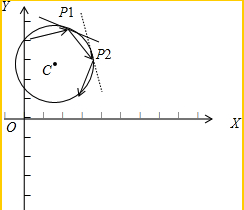

（2）①由题意：∠1=∠2，∠APB=90°，
∴∠1=45°，
∴反射光与切线的夹角为45°．
②由题意：这些反射点组成的多边形是正十二边形，
∴入射光线与反射光线夹角为150°，
∴∠AOP1=30°，∵OP1=1，
∴P1（-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）．
（3）如图：当反射光PA∥X轴时，反射光线与坐标轴没有交点．
作PD⊥OC，PN⊥OM垂足分别为M，N，设PD=m．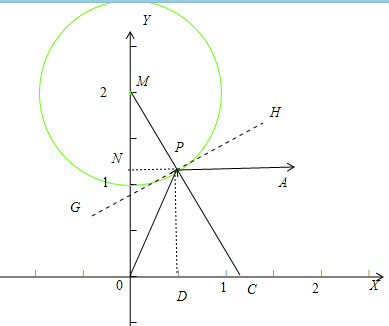
∵∠GPO=∠HPA，∠GPC=∠HPC=90°，
∴∠OPC=∠APC=∠PCO，∴OP=OC，
在RT△PON中，∵ON=PD=m，PN²=1-（2-m）²，
∴PO²=m²+1-（2-m）²，
∵PD∥OM，∵$\frac{PD}{OM}=\frac{CP}{CM}$，∴CP=$\frac{m}{2-m}$，
CD²=（$\frac{m}{2-m}$）²-m²，
∴OC=PN+CD，
OC²=（$\sqrt{1-（2-m）^{2}}$+$\sqrt{（\frac{m}{2-m}）^{2}-{m}^{2}}$）²，
由：PO²=OC²得到：（$\frac{m}{2-m}$）²-m²=（$\sqrt{1-（2-m）^{2}}$+$\sqrt{（\frac{m}{2-m}）^{2}-{m}^{2}}$）²，
∴m1=2-$\frac{\sqrt{2}}{2}$，（m2=2+$\frac{\sqrt{2}}{2}$，m3=4，不合题意舍弃），
∴根据左右对称性得到：满足条件的反射点P的纵坐标：1$≤m＜2-\frac{\sqrt{2}}{2}$．

点评 这是个几何，代数综合题．考查的知识点比较多，用到数形结合的思想，要求作图能力强，学会用方程的思想去思考．