题目内容
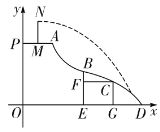
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,其中
两点,其中![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() ,连接
,连接![]() .
.
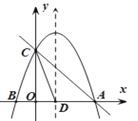
(1)求抛物线和直线![]() 的解析式:
的解析式:
(2)若抛物线上存在一点![]() ,使
,使![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上是否存在一点![]() ,使线段
,使线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,且
,且![]() 恰好落在抛物线上?若存在,求出点
恰好落在抛物线上?若存在,求出点![]() 的坐标;若不存在,请说叫理由.
的坐标;若不存在,请说叫理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 和
和![]() .
.
【解析】
(1)先利用待定系数法求出抛物线的解析式,从而可求出点C的坐标,再利用待定系数法即可求出直线AC的解析式;
(2)先根据二次函数的性质可得![]() ,从而可得
,从而可得![]() ,再根据平行线的性质可知过点B作
,再根据平行线的性质可知过点B作![]() ,与抛物线的交点即为其他符合条件的点P,然后联立直线BE和抛物线的解析式求解即可得;
,与抛物线的交点即为其他符合条件的点P,然后联立直线BE和抛物线的解析式求解即可得;
(3)分当点Q在x轴的上方和当点Q在x轴的下方两种情况,再分别根据直角三角形的性质、三角形全等的判定定理与性质、二次函数的性质求解即可得.
(1)把![]() ,
,![]() 代入
代入![]() 得
得![]()
解得![]()
∴抛物线的解析式为![]()
当![]() 时,
时,![]()
∴点![]() 的坐标是
的坐标是![]()
把![]() ,
,![]() 代入
代入![]() 得
得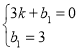
解得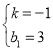
∴直线![]() 的解析式为
的解析式为![]() ;
;
(2)∵![]()
∴![]()
如图,过![]() 点作
点作![]()
由平行线的性质可知,直线BE上的点到AC的距离均相等
则直线BE上的任意一点与点A、C组成的三角形的面积均等于![]() 的面积,均为
的面积,均为![]() 面积的2倍
面积的2倍
![]()
![]() 设直线BE的解析式为
设直线BE的解析式为![]()
将点![]() 代入得
代入得![]() ,解得
,解得![]()
则直线BE的解析式为![]()
联立![]() ,解得
,解得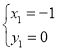 ,
,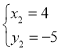
故符合条件的点![]() 的坐标为
的坐标为![]() ,
,![]() ;
;
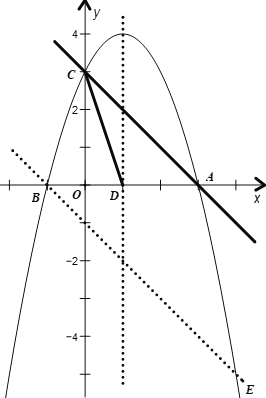
(3)由题意,分以下两种情况:
①当点Q在x轴的上方
设![]() 与对称轴交点为
与对称轴交点为![]()
由![]() 可知,抛物线的对称轴为
可知,抛物线的对称轴为![]()
令![]() 代入
代入![]() 得
得![]()
∴![]() 坐标为
坐标为![]()
∴![]()
∴![]()
∴![]()
∴![]() 即为所求
即为所求
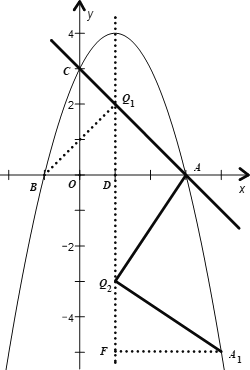
②当点Q在x轴的下方
如图,过点![]() 作
作![]() 于点F
于点F
![]()
![]()
![]()
由旋转的性质得:![]()
在![]() 和
和![]() 中,
中,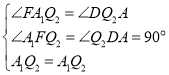
![]()
![]()
设![]() ,则
,则![]()
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,即
,即![]()
将![]() 代入
代入![]() 得
得![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
即![]()
![]() 的坐标为
的坐标为![]()
综上,点![]() 的坐标为
的坐标为![]() 和
和![]() .
.

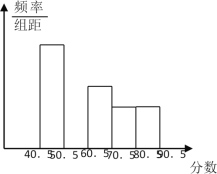
【题目】为弘扬中华优秀传统文化,某校组织了“古诗词”知识竞赛,由九年级的若干名学生参加选拔赛,从中选出10名优胜者,下面是对参赛学生成绩的不完整统计.
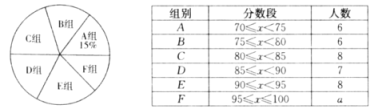
(1)统计表中,![]() =_____;各组人数的中位数是_____;统计图中,
=_____;各组人数的中位数是_____;统计图中,![]() 组所在扇形的圆心角是_____°;
组所在扇形的圆心角是_____°;
(2)李明同学得了88分,他说自己在参加选拔赛的同学中属于中午偏上水平,你认为他说的有道理吗?为什么?
(3)选出的10名优胜者中,男生、女生的分布情况如下表.
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人数 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人数 | 1 | 0 | 0 | 2 | 1 | 1 |
若从中任选1名男生和1名女生代表学校参加全区的比赛,请有列表法或画树状图法求男生和女生都出在四班的概率.