题目内容
 如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=| 6 |
| x |
| A、3 | B、6 | C、12 | D、24 |
考点:反比例函数综合题
专题:
分析:过点P作PE⊥x轴于点E,作PF⊥y轴于点F,根据垂径定理可得:OF=
OB,OE=
OA,设点P的坐标为(x,y),根据条件可得到xy=6,OA=2x,OB=2y,从而可求出△AOB的面积.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:过点P作PE⊥x轴于点E,作PF⊥y轴于点F,如图所示.
根据垂径定理可得:OF=BF=
OB,OE=AE=
OA.
设点P的坐标为(x,y),
∵点P是反比例函数y=
(x>0)图象上的一点,
∴xy=6,OA=2OE=2x,OB=2OF=2y,
∴S△AOB=
OA•OB=
•2x•2y=2xy=12.
故选:C.

根据垂径定理可得:OF=BF=
| 1 |
| 2 |
| 1 |
| 2 |
设点P的坐标为(x,y),
∵点P是反比例函数y=
| 6 |
| x |
∴xy=6,OA=2OE=2x,OB=2OF=2y,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查了反比例函数图象上点的坐标特征、垂径定理等知识,运用整体思想是解决本题的关键.

练习册系列答案
相关题目
在数轴上,点A、B对应的数分别为-2,
,且A、B两点关于原点对称,则x的值为( )
| x+1 |
| x |
| A、2 | B、-2 | C、1 | D、-1 |
 如图是某几何体的三视图.
如图是某几何体的三视图.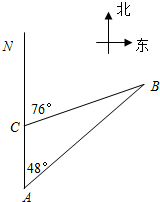 如图,一艘货轮以30海里/时的速度在海面上航行,当它行驶到A处时,发现在它的北偏东48°方向有一港口B,货轮继续向北航行40分钟后到达C处,发现港口B在它的北偏东76°方向上,若货轮急需到港口B补充供给,请求出C处与港口B的距离CB的长度.(结果保留整数)
如图,一艘货轮以30海里/时的速度在海面上航行,当它行驶到A处时,发现在它的北偏东48°方向有一港口B,货轮继续向北航行40分钟后到达C处,发现港口B在它的北偏东76°方向上,若货轮急需到港口B补充供给,请求出C处与港口B的距离CB的长度.(结果保留整数) 如图所示,河堤横断面迎水坡AB的坡比是1:3,堤高BC=5m,则坡面AB的长度是
如图所示,河堤横断面迎水坡AB的坡比是1:3,堤高BC=5m,则坡面AB的长度是