题目内容
如图,n+1个边长为1的等边三角形一边均在同一直线上,设△BMN面积为S,△B1M1N1面积为S1,△B2M2N2的 面积为S2,…,△BnMnNn的面积记为Sn,则:
面积为S2,…,△BnMnNn的面积记为Sn,则:
①S=
,
②请你计算归纳S1,S2,…,可得S1+S2+…+S2011=
.
 面积为S2,…,△BnMnNn的面积记为Sn,则:
面积为S2,…,△BnMnNn的面积记为Sn,则:①S=
| ||
| 8 |
| ||
| 8 |
②请你计算归纳S1,S2,…,可得S1+S2+…+S2011=
| 2011 |
| 16104 |
| 3 |
| 2011 |
| 16104 |
| 3 |
分析:①连接BB1,由于△BAN是边长为1的等边三角形,则S△BAN=
.由于BN∥B1A且BN=B1A,则四边形BNAB1是平行四边形,根据平行四边形的对角线互相平分得出BM=AM,则S=
S△BAN=
;
②连接B1、B2、B3…Bn点,显然它们共线且平行于NAn,则B1B2∥NA,△B1B2N1∽△ANN1,△B1B2M1∽△A2NM1,根据相似三角形的性质得出B1N1:AN1=B1B2:AN=1,B1M1:M1A2=B1B2:A2N=1:2,然后根据三角形的面积公式得出S1=
×
S△BAN,同理,可求出S2=
×
S△BAN,…,S2011=
×
S△BAN,最后将它们相加即可.
| ||
| 4 |
| 1 |
| 2 |
| ||
| 8 |
②连接B1、B2、B3…Bn点,显然它们共线且平行于NAn,则B1B2∥NA,△B1B2N1∽△ANN1,△B1B2M1∽△A2NM1,根据相似三角形的性质得出B1N1:AN1=B1B2:AN=1,B1M1:M1A2=B1B2:A2N=1:2,然后根据三角形的面积公式得出S1=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2012 |
| 1 |
| 2013 |
解答:解:①连接BB1.
∵△BAN是边长为1的等边三角形,∴S△BAN=
.
∵∠BNA=∠B1AA2=60°,∴BN∥B1A,
∵BN=B1A,∴四边形BNAB1是平行四边形,
∴BM=AM,
 ∴S=
∴S=
S△BAN=
;
②连接B1、B2、B3…Bn点,显然它们共线且平行于NAn,则B1B2∥NA,
∴△B1B2N1∽△ANN1,△B1B2M1∽△A2NM1,
∴B1N1:AN1=B1B2:AN=1,B1M1:M1A2=B1B2:A2N=1:2,
∴B1N1=
AB1,B1M1=
A2B1,
∴S1=
×B1N1×B1M1sin∠N1B1M1=
×
AB1×
A2B1sin∠N1B1M1=
×
S△BAN=(
-
)S△BAN,
同理,△B2B3N2∽△A2NN2,△B2B3M2∽△A3NM2,
∴B2N2:A2N2=B2B3:A2N=1:2,B2M2:M2A3=B2B3:A3N=1:3,
∴B2N2=
A2B2,B2M2=
A3B2,
∴S2=
×B2N2×B2M2sin∠N2B2M2=
×
A2B2×
A3B2=
×
S△BAN=(
-
)S△BAN,
…,
∴S2011=
×
S△BAN=(
-
)S△BAN,
∴S1+S2+…+S2011=(
-
)S△BAN+(
-
)S△BAN+…+(
-
)S△BAN=(
-
)S△BAN=
×
=
.
故答案为:①
;②
.
∵△BAN是边长为1的等边三角形,∴S△BAN=
| ||
| 4 |
∵∠BNA=∠B1AA2=60°,∴BN∥B1A,
∵BN=B1A,∴四边形BNAB1是平行四边形,
∴BM=AM,
 ∴S=
∴S=| 1 |
| 2 |
| ||
| 8 |
②连接B1、B2、B3…Bn点,显然它们共线且平行于NAn,则B1B2∥NA,
∴△B1B2N1∽△ANN1,△B1B2M1∽△A2NM1,
∴B1N1:AN1=B1B2:AN=1,B1M1:M1A2=B1B2:A2N=1:2,
∴B1N1=
| 1 |
| 2 |
| 1 |
| 3 |
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
同理,△B2B3N2∽△A2NN2,△B2B3M2∽△A3NM2,
∴B2N2:A2N2=B2B3:A2N=1:2,B2M2:M2A3=B2B3:A3N=1:3,
∴B2N2=
| 1 |
| 3 |
| 1 |
| 4 |
∴S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
…,
∴S2011=
| 1 |
| 2012 |
| 1 |
| 2013 |
| 1 |
| 2012 |
| 1 |
| 2013 |
∴S1+S2+…+S2011=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2012 |
| 1 |
| 2013 |
| 1 |
| 2 |
| 1 |
| 2013 |
| 2011 |
| 4026 |
| ||
| 4 |
| 2011 |
| 16104 |
| 3 |
故答案为:①
| ||
| 8 |
| 2011 |
| 16104 |
| 3 |
点评:本题主要考查相似三角形的判定和性质、等边三角形的定义和性质、三角形的面积公式等知识点、本题关键在于作好辅助线,得到相似三角形,求出相似比,就很容易得出答案了,意在提高同学们总结归纳的能力.

练习册系列答案
相关题目
 如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.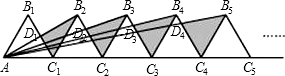

 已知△ABC,AB=3,BC=
已知△ABC,AB=3,BC=