题目内容
19. 如图,在平面直角坐标系xOy中,直线l的表达式是y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,点B4的坐标为(8$\sqrt{3}$,8),OA2015=22014.
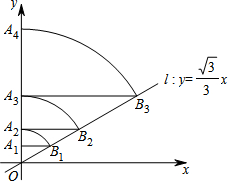
如图,在平面直角坐标系xOy中,直线l的表达式是y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,按此作法进行下去,点B4的坐标为(8$\sqrt{3}$,8),OA2015=22014.
分析 先根据一次函数方程式求出B1点的坐标,在根据B1点的坐标求出A2点的坐标,由此得到点A4的坐标,以此类推总结规律便可求出点An的坐标,进而求得OA2015的值.
解答 解:直线y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,可知B1点的坐标为($\sqrt{3}$,1),
以原点O为圆心,OB1长为半径画弧交y一轴于点A2,OA2=OB1=2OA1=2,点A2的坐标为(0,2),
这种方法可求得B2的坐标为(2$\sqrt{3}$,2),
故点A3的坐标为(0,4),B3的坐标为(4$\sqrt{3}$,4),
点A4的坐标为(0,8),B4的坐标为(8$\sqrt{3}$,8),
此类推便可求出点An的坐标为(0,2n-1).
所以点A2015的坐标为(0,22014).
所以OA2015=22014.
故答案为:(8$\sqrt{3}$,8),22014.
点评 本题主要考查了一次函数的应用,做题时要注意数形结合思想的运用,是各地的中考热点,学生在平常要多加训练,属于中档题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
10.$\sqrt{(-3)^{2}}$的值等于( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $\sqrt{3}$ |
14.甲、乙、丙、丁四位同学角逐“汉字听写大赛”的决赛资格,表中统计了他们五次测试成绩的平均分和方差.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全市“汉字听写大赛”,那么应选( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均分 | 80 | 80 | 85 | 85 |
| 方 差 | 59 | 41 | 54 | 42 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
11.某园林队计划由6名工人对200平方米的区域进行绿化,由于施工时增加了2名工人,结果比计划提前3小时完成任务,若每人每小时绿化面积相同,求每人每小时的绿化面积.设每人每小时的绿化面积为x平方米,列出满足题意的方程是( )
| A. | $\frac{200}{6x}$-$\frac{200}{(6+2)x}$=3 | B. | $\frac{200}{(6+2)x}$-$\frac{200}{6x}$=3 | C. | $\frac{200}{6x}$-$\frac{200}{2x}$=3 | D. | $\frac{200}{2x}$-$\frac{200}{6x}$=3 |
8.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.在函数y=$\frac{{\sqrt{x+1}}}{x-2}$中,自变量x的取值范围是( )
| A. | x≤-1 | B. | x≥-1 | C. | x≤-1且x≠2 | D. | x≥-1且x≠2 |
 如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,说说为什么∠DAE=$\frac{1}{2}$(∠C-∠B),写出你的推理过程.
如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,说说为什么∠DAE=$\frac{1}{2}$(∠C-∠B),写出你的推理过程.