题目内容
14.(1)$({-\frac{2}{3}+\frac{3}{4}-\frac{5}{6}})×({-12})$(2)-14-(1-0.5)×$\frac{1}{3}×[{2-{{({-3})}^2}}]$
(3)x-(2x-3y)+2(-3x+4y)
(4)3x2+[2x+2-(-x2+4x)]-1.
分析 (1)利用乘法分配律将原式展开,分别相乘后再相加;(2)按照有理数混合运算的顺序和法则,一步步继续运算即可得出结论;
(3)去掉小括号,合并同类项即可得出结论;(4)去掉括号,合并同类项即可得出结论.
解答 解:(1)原式=(-$\frac{2}{3}$)×(-12)+$\frac{3}{4}$×(-12)+(-$\frac{5}{6}$)×(-12),
=8-9+10,
=9.
(2)原式=-14-$\frac{1}{2}$×$\frac{1}{3}$×(2-9),
=-14-$\frac{1}{2}$×$\frac{1}{3}$×(-7),
=-1+$\frac{7}{6}$,
=$\frac{1}{6}$.
(3)原式=x-2x+3y-6x+8y,
=11y-7x.
(4)原式=3x2+(2x+2+x2-4x)-1,
=3x2+2+x2-2x-1,
=4x2-2x+1.
点评 本题考查了有理数的混合运算以及整式的加减法,解题的关键是:(1)按照乘法分配律展开去分母;(2)牢记有理数混合运算的顺序;(3)(4)去括号,合并同类项.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5. 如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
 如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 70° |
6.下列变形正确的是( )
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{-x+y}{x-y}$=-1 | C. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | D. | $\frac{x+2}{x+3}$=$\frac{2}{3}$ |
3.点(1,2)在下列哪个函数图象上( )
| A. | y=x-3 | B. | y=2x+2 | C. | y=2x | D. | y=x2+2 |
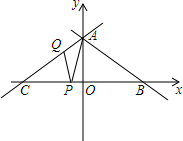 如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°.
如图,直线AB:y=-$\frac{\sqrt{3}}{3}$x+$\frac{8\sqrt{3}}{3}$交坐标轴于A、B两点,直线AC与AB关于y轴对称,交x轴于点C.点P、Q分别是线段BC、AC上两个动点,且∠APQ始终等于30°. a,b,c三个数在数轴上的位置如图所示,化简:|a-b|-|a+c|-|c-b|.
a,b,c三个数在数轴上的位置如图所示,化简:|a-b|-|a+c|-|c-b|.