题目内容
17.(1)如果将一副三角板△ABC和△BED如图1放置,其中∠BAC=∠BDE=90°,BD=ED,AD∥BE,AC与ED交于点P,求证:AB=AP.(2)如果将一副三角板△ABC和△BED如图2放置,其中∠BAC=∠BDE=90°,BD=ED,AD∥BE,AC与ED的延长线交于点P,试问△ABP是轴对称图形吗?请说明理由.
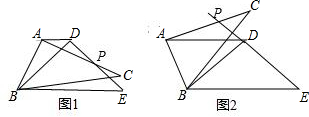
分析 (1)过点A作AF⊥AD,交DB于点F,证得△BAF≌△PAD,可以证明BA=AP;
(2)过点A作AF⊥AD,交DB的延长线于点F,证得△BAF≌△PAD,可以证明BA=AP,从而证得△ABP是轴对称图形;
解答 (1)证明:如图1,过点A作AF⊥AD,交DB于点F,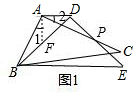
则△ADF为等腰直角三角形,
∴DA=AF.
∵∠1+∠FAP=90°,∠FAP+∠2=90°,
∴∠1=∠2.
在△BAF与△PDA中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AF=AD}\\{∠AFB=∠ADP=135°}\end{array}\right.$,
∴△BAF≌△PAD(ASA),
∴AB=AP.
(2)证明:如图2,过点A作AF⊥AD,交DB的延长线于点F,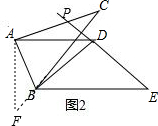
则△ADF为等腰直角三角形,
∴AD=AF.
∵∠FAB+∠DAB=90°,∠DAB+∠CAD=90°,
∴∠FAB=∠CAD.
在△BAF与△PAD中,
$\left\{\begin{array}{l}{∠FAB=∠CAD}\\{AF=AD}\\{∠AFB=∠ADP=45°}\end{array}\right.$,
∴△BAF≌△PAD(ASA),
∴AB=AP,
∴△ABP是轴对称图形.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、平行线的性质等知识点,作辅助线构造全等三角形是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,△ABC中,CA=CB,D、E分别为AB、BC上一点,且CD=CE,若∠ACD=20°,求∠BDE的度数.
如图,△ABC中,CA=CB,D、E分别为AB、BC上一点,且CD=CE,若∠ACD=20°,求∠BDE的度数.