题目内容
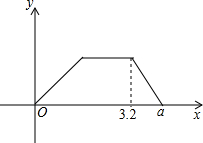一辆货车从甲地匀速驶往乙地，到达后用了半小时卸货，随即匀速返回，已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍．货车离甲地的距离y（千米）关于时间x（小时）的函数图象如图所示．则a=考点：一次函数的应用
专题：数形结合
分析：由图可知，从一辆货车从甲地匀速驶往乙地，到达所用时间为3.2-0.5=2.7小时，而返回的速度是它从甲地驶往乙地的速度的1.5倍，路程一样，回到甲地的时间也就是原来时间的
，求得返回用的时间为2.7÷1.5=1.8小时，由此求得a=3.2+1.8=5小时．
| 1 |
| 1.5 |
解答：解：由题意可知：
从甲地匀速驶往乙地，到达所用时间为3.2-0.5=2.7小时，
返回的速度是它从甲地驶往乙地的速度的1.5倍，
返回用的时间为2.7÷1.5=1.8小时，
所以a=3.2+1.8=5小时．
故答案为：5．
从甲地匀速驶往乙地，到达所用时间为3.2-0.5=2.7小时，
返回的速度是它从甲地驶往乙地的速度的1.5倍，
返回用的时间为2.7÷1.5=1.8小时，
所以a=3.2+1.8=5小时．
故答案为：5．
点评：此题考查利用函数图象解决有关实际问题，注意利用路程、时间、速度之间三者的关系解决问题．
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
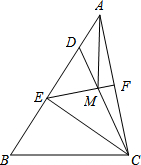如图，在△ABC中，点D在AB上，且CD=CB，点E为BD的中点，点F为AC的中点，连结EF交CD于点M，连接AM．
如图，已知四边形ABCD是正方形，点E在DC上，将△ADE经顺时针旋转后与△ABF重合，再将△ABF向右平移后与△DCH重合．
如图，∠1、∠2、∠A的大小关系是
如图．将平面内Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC．若AC=2，BC=1，则线段BE的长为
如图，在直角梯形ABCD中，AB=BC=6，点E为BC边上一点，且∠EAD=45°，ED=5，则△ADE的面积为