题目内容
19.先化简,再求值($\frac{4}{x+3}$-1)÷$\frac{{x}^{2}-1}{x+3}$,其中x=2cos30°-tan45°.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,利用特殊角的三角函数值求出x的值,代入计算即可求出值.
解答 解:原式=-$\frac{x-1}{x+3}$•$\frac{x+3}{(x+1)(x-1)}$=-$\frac{1}{x+1}$,
当x=2×$\frac{\sqrt{3}}{2}$-1=$\sqrt{3}$-1时,原式=-$\frac{\sqrt{3}}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.“相等的角是对顶角”是( )
| A. | 定义 | B. | 公理 | C. | 假命题 | D. | 定理 |
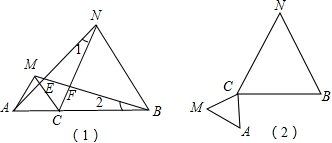
 已知数a、b、c在数轴上的位置如图所示,化简|a|+|b|+|a+b|-|b-c|.
已知数a、b、c在数轴上的位置如图所示,化简|a|+|b|+|a+b|-|b-c|.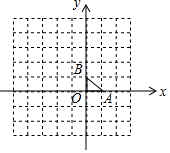 如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心,此时,M是线段PQ的中点.如图,在直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0),点列P1,P2,P3…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称…对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),则P2的坐标是(1,-1),P2014的坐标是(1,-3).
如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心,此时,M是线段PQ的中点.如图,在直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0),点列P1,P2,P3…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称…对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),则P2的坐标是(1,-1),P2014的坐标是(1,-3).