题目内容
在凸四边形ABCD中,AB=AD=BC,∠BAD=90°,AC把四边形ABCD分成两个等腰三角形,则∠ABC的度数为 .
考点:等腰三角形的判定
专题:分类讨论
分析:首先根据题意画出图形,然后由AC把四边形ABCD分成两个等腰三角形,可以得出△ACD是等腰三角形,从图1,图2,图3三种情况运用等边三角形的性质,正方形的性质和30°的直角三角形的性质就可以求出∠ABC的度数.
解答: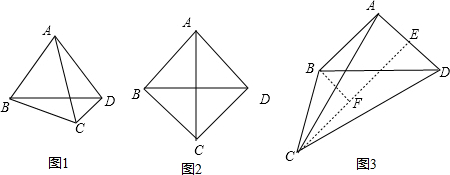 解:∵AC把四边形ABCD分成两个等腰三角形,
解:∵AC把四边形ABCD分成两个等腰三角形,
∴△ACD是等腰三角形.
如图1,当AD=AC时,
∵AB=AD=BC,
∴AB=AC=BC,
∴△ABC是正三角形,
∴∠ABC=60°;
如图2,当AD=CD时,
∵AB=AD=BC,
∴AB=AD=BC=CD,
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠ABC=90°;
如图3,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,
∵AC=CD,CE⊥AD,
∴AE=
AD,∠ACE=∠DCE.
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形,
∴BF=AE.
∵AB=AD=BC,
∴BF=
BC,
∴∠BCF=30°.
∵AB∥CE,
∴∠ABC=180°-∠BCF=150°,
综上所述,∠ABC的度数为60°、90°、150°.
故答案为:60°、90°、150°.
 解:∵AC把四边形ABCD分成两个等腰三角形,
解:∵AC把四边形ABCD分成两个等腰三角形,∴△ACD是等腰三角形.
如图1,当AD=AC时,
∵AB=AD=BC,
∴AB=AC=BC,
∴△ABC是正三角形,
∴∠ABC=60°;
如图2,当AD=CD时,
∵AB=AD=BC,
∴AB=AD=BC=CD,
∵∠BAD=90°,
∴四边形ABCD是正方形,
∴∠ABC=90°;
如图3,当AC=CD时,过点C作CE⊥AD于E,过点B作BF⊥CE于F,
∵AC=CD,CE⊥AD,
∴AE=
| 1 |
| 2 |
∵∠BAD=∠AEF=∠BFE=90°,
∴四边形ABFE是矩形,
∴BF=AE.
∵AB=AD=BC,
∴BF=
| 1 |
| 2 |
∴∠BCF=30°.
∵AB∥CE,
∴∠ABC=180°-∠BCF=150°,
综上所述,∠ABC的度数为60°、90°、150°.
故答案为:60°、90°、150°.
点评:此题考查了等腰三角形的性质、矩形的性质、正方形的性质以及含30°角的直角三角形的性质.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某商品2010年比2009年涨价5%,2011年又比2010年涨价10%,预计2012年比2011年降价12%,则2012年比2009年( )
| A、涨价3% |
| B、涨价1.64% |
| C、涨价1.2% |
| D、降价1.2% |
若cosα=
,则锐角α的度数是( )
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |