题目内容
4.已知直角三角形斜边为(2$\sqrt{6}$+$\sqrt{3}$)cm,一条直角边长为($\sqrt{6}$+2$\sqrt{3}$)cm,求另一条直角边的长.分析 直接利用勾股定理结合二次根式乘法运算法则化简求出即可.
解答 解:∵直角三角形斜边为(2$\sqrt{6}$+$\sqrt{3}$)cm,一条直角边长为($\sqrt{6}$+2$\sqrt{3}$)cm,
∴另一条直角边的长为:$\sqrt{(2\sqrt{6}+\sqrt{3})^{2}-(\sqrt{6}+2\sqrt{3})^{2}}$=$\sqrt{9}$=3.
答:另一条直角边的长为3.
点评 此题主要考查了二次根式的应用,熟练应用二次根式的乘法运算法则是解题关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
12.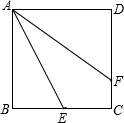 如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )
如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )
 如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )
如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
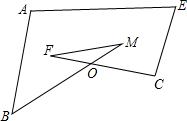 课堂上,老师提出一个问题:如图,求∠A+∠ABO+∠M+∠F+∠ECF+∠E的度数.独立思考:
课堂上,老师提出一个问题:如图,求∠A+∠ABO+∠M+∠F+∠ECF+∠E的度数.独立思考: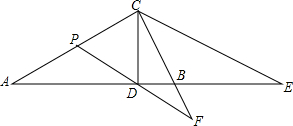 如图,CD是△ABC的高,∠ACB=90°,∠DCB=∠ECB,P是AC的中点,PD的延长线交BC的延长线于点F,说明:AC•CE=2PF•CD.
如图,CD是△ABC的高,∠ACB=90°,∠DCB=∠ECB,P是AC的中点,PD的延长线交BC的延长线于点F,说明:AC•CE=2PF•CD.