Question

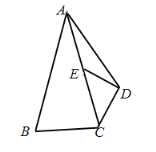
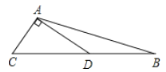
【题目】如图，在△ABC中，点D是BC的中点，DA⊥AC，tan∠BAD=，AB=，则BC的长度为______．

Answer 1

【答案】

【解析】

作DE∥AC交AB于E，如图，根据平行线的性质得∠ADE＝90，由点D是BC的中点得到DE为△ABC的中位线，则DE＝AC，AE＝BE＝AB＝2，在Rt△ADE中，根据正切的定义得tan∠EAD＝＝，设DE＝x，则AD＝2x，根据勾股定理得（2x）2＋x2＝（2）2，解得x＝2，则DE＝2，AD＝4，所以AC＝4，然后根据勾股定理计算出CD＝，再利用BC＝2CD计算即可．

作DE∥AC交AB于E，如图，

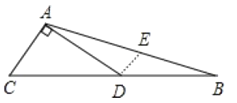
∵DA⊥AC，

∴DE⊥AD，

∴∠ADE＝90，

∵点D是BC的中点，

∴DE为△ABC的中位线，

∴DE＝AC，AE＝BE＝AB＝2，

在Rt△ADE中，tan∠EAD＝＝，

设DE＝x，则AD＝2x，

∵AD2＋DE2＝AE2，

∴（2x）2＋x2＝（2）2，解得x＝2，

∴DE＝2，AD＝4，

∴AC＝2DE=4，

∴CD＝，

∴BC＝2CD＝

故答案为：．