题目内容
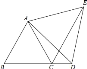
【题目】如图,已知一次函数
的图象 与x轴、y轴分别交于点A,B.
(1)求点A,B的坐标;
(2)M为ー次函数y=x+3的图象上一点,若 △ABM与△ABO的面积相等,求点M的坐标;
(3)Q为y轴上的一点，若三角形ABQ为等腰三角形 ，请直接写出点Q的坐标.
【答案】（1）A（6,0） B(0，3);(2)M(-2，1)或（2,5）;（3）Q的坐标（0，-3） （0，
+3）,（0,3-）,（0，-
）
【解析】
（1）分别计算函数值为0定义的自变量和自变量为0对应的函数值可得到A、B点的坐标；
（2）利用同底等高面积相等求解，先确定点M在直线y=-
x或y=-x+6上，然后通过解方程组求M点的坐标；
（3）先计算出AB，分类讨论：以A为顶点得到Q（0，-3），以B为顶点得到Q（0，+3）或（0，-+3），以Q为顶点利用QA=QB可求Q点坐标．
解：（1）当y=0时，-x+3=0，解得x=6，则A（6，0），
当x=0时，y=-x+3=3，则B（0，3）；
（2）∵△ABM与△ABO的面积相等，
∴M点到直线AB的距离与O点到AB的距离相等，
∴点M在直线y=-x或y=-x+6上，
解方程组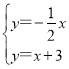
得
解方程组
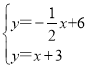得
∴M点的坐标为（-2，1）或（2，5）；
（3）AB=
，
当AQ=AB，则Q（0，-3），
当BQ=BA=
时，则Q（0，+3）或（0，-+3），
当QA=QB时，作AB的垂直平分线交y轴于Q，如图，
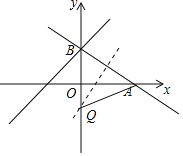
设Q（0，t），
∵QA2=62+t2，QB2=（3-t）2，
∴62+t2=（3-t）2，解得t=-，
∴此时Q（0，-）．
综上所述，Q点坐标为Q（0，-3）或Q（0，+3）或（0，-+3）或Q（0，-）．
练习册系列答案
相关题目
