Question

【题目】如图,在长方形纸片中, ,折叠纸片,使得点落在边上的点处,折痕为,点分别在边和上,当点恰好是边的中点时,点与点重合,若在折叠过程中,则等于________.

Answer 1

【答案】9

【解析】

先求出BC的长，过点N作HN⊥CD，由勾股定理可求NB的长，由等腰三角形的性质可求PC的长，即可求PD的长．

如图1，当点P恰好是CD边的中点时，点N与点B重合，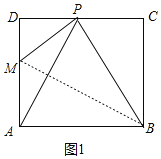

∵点P是CD的中点，
∴CP=CD=6cm，
由折叠的性质可得：AB=PB=12cm，
∴BC=，
如图2，折叠过程中NP=NC，过点N作HN⊥CD，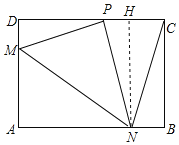

由折叠的性质可得：AN=PN=NC，
∵NB2+BC2=NC2，
∴NB2+108=（12-NB）2，
∴NB=cm，
∵NH⊥CD，∠ABC=∠BCD=90°，
∴四边形BCHN是矩形，
∴HC=BN=cm，
∵NC=NP，NH⊥CD，
∴PC=2HC=3cm，
∴PD=CD-PC=9cm，
故答案为：9cm．