题目内容
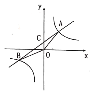
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
【答案】A
【解析】∵∠C=90°,BC=2cm,∠A=30°,
∴AB=4,
由勾股定理得:AC=2![]() ,
,
∵四边形DEFG为矩形,∠C=90,
∴DE=GF=2![]() ,∠C=∠DEF=90°,
,∠C=∠DEF=90°,
∴AC∥DE,
此题有三种情况:
(1)当0<x<2时,AB交DE于H,如图
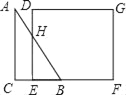
∵DE∥AC,
∴![]() ,
,
即![]() ,
,
解得:EH=![]() x,
x,
所以y=![]()
![]() xx=
xx=![]() x2,
x2,
∵x 、y之间是二次函数,
所以所选答案C错误,答案D错误,
∵a=![]() >0,开口向上;
>0,开口向上;
(2)当2≤x≤6时,如图,
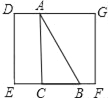
此时y=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
(3)当6<x≤8时,如图,设△ABC的面积是s1,△FNB的面积是s2,
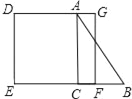
BF=x﹣6,与(1)类同,同法可求FN=![]() X﹣6
X﹣6![]() ,
,
∴y=s1﹣s2,
=![]() ×2×2
×2×2![]() ﹣
﹣![]() ×(x﹣6)×(
×(x﹣6)×(![]() X﹣6
X﹣6![]() ),
),
=﹣![]() x2+6
x2+6![]() x﹣16
x﹣16![]() ,
,
∵﹣![]() <0,
<0,
∴开口向下,
所以答案A正确,答案B错误,
故选:A.

练习册系列答案
相关题目