题目内容
9.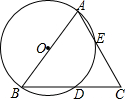 如图,AB=AC,AB是直径,求证:BC=2DE.
如图,AB=AC,AB是直径,求证:BC=2DE.
分析 连接AD、DE,由直径可知AD⊥BC,由等腰三角形的性质可知:BD=2BD,∠BAD=∠DAC,再根据圆周角定理可知BD=DE,从而得证.
解答 证明:连接AD、DE
∵AB为⊙O的直径
∴∠ADB=90°
∴AD⊥BC
∵AB=AC
∴∠BAD=∠DAC; BC=2BD=2DC
由圆周角定理可知:BD=DE
∴BC=2DE.
点评 本题考查圆周角定理,解题的关键是利用等腰三角形的三线合一性质求出BD=2BD,∠BAD=∠DAC,本题属于中等题型.

练习册系列答案
相关题目
1.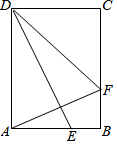 在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )
在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )
 在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )
在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )| A. | $\sqrt{2}-1$ | B. | 0.5 | C. | $\frac{2}{3}$ | D. | 1 |
19.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送2450张照片,如果全班有x名同学,根据题意,列出方程为( )
| A. | x(x+1)=2450 | B. | x(x-1)=2450 | C. | $\frac{1}{2}$x(x+1)=2450 | D. | $\frac{1}{2}$x(x-1)=2450 |
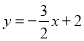 与x轴、y轴分别交于点A、B两点,下列各点向左平移2个单位后能落在
与x轴、y轴分别交于点A、B两点,下列各点向左平移2个单位后能落在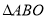 内部的是( )
内部的是( )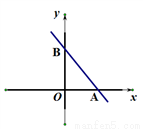
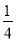 ) B. (2,2) C. (4,1) D. (3,1)
) B. (2,2) C. (4,1) D. (3,1)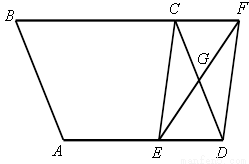
 如图,在△ABC中,∠C=90°,∠A=α,D是边AC上一点,且∠BDC=β,AD=a,求BC的长.(用含a、α、β的式子表示)
如图,在△ABC中,∠C=90°,∠A=α,D是边AC上一点,且∠BDC=β,AD=a,求BC的长.(用含a、α、β的式子表示) 观察图形,利用图形面积关系用写出一个代数恒等式.
观察图形,利用图形面积关系用写出一个代数恒等式.