题目内容
12. 如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A,B两点重合,AE⊥AB,AE=BD,连接DE、DC
如图,Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,且不与A,B两点重合,AE⊥AB,AE=BD,连接DE、DC(1)求证:△ACE≌△BCD;
(2)猜想CD与CE的数量关系和位置关系,并说明理由.
分析 (1)由已知可得△ABC是等腰直角三角形,由AE⊥AB即可得到∠1=∠B,从而可利用SAS判定△ACE≌△BCD.
(2)根据已知可猜想CE=CD,CE⊥CD,由第一问可得CE=CD,∠3=∠4,根据等角的性质可推出∠ECD=90°,从而得到答案.
解答 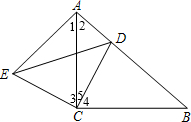 (1)证明:∵∠ACB=90°,AC=BC,
(1)证明:∵∠ACB=90°,AC=BC,
∴∠B=∠2=45°.
∵AE⊥AB,
∴∠1+∠2=90°.
∴∠1=45°.
∴∠1=∠B.
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AE=BD}\\{∠1=∠B}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△BCD(SAS).
(2)猜想:CE=CD,CE⊥CD;理由说明:
解:∵△ACE≌△BCD,
∴CE=CD,∠3=∠4.
∵∠4+∠5=90°,
∴∠3+∠5=90°.
即∠ECD=90°.
∴CE⊥CD.
点评 本题考查了全等三角形的判定和性质,以及学生对全等三角形的判定方法及等腰直角三角形的判定的综合运用.

练习册系列答案
相关题目
7.国际上常用恩格尔系数(记作n)来衡量一个国家和地区人民生活水平的状况,它的计算公式为:n=$\frac{食品消费支出总额}{消费支出总额}$×100%,各类家庭的恩格尔系数如下表所示:
我市对某乡镇农村家庭进行抽样调查发现:从1999年~2009年这10年间,该乡每户家庭消费支出总额每年平均增加1150元,其中食品消费支出总额平均每年增加300元.1999年该乡农民家庭平均刚达到温饱水平,到2009年该乡农民家庭平均已达富裕水平,则2009年该乡农民家庭平均食品消费最多支出为9000元元.
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 | 最富裕 |
| n | n>60% | 50%<n≤60% | 40%<n≤50% | 30%<n≤40% | n≤30% |
2.下列计算正确的是( )
| A. | 2a+3b=5ab | B. | (x+2)2=x2+4 | C. | (-1)0=1 | D. | (ab3)2=ab6 |
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点M,OA=3,tan∠AMO=$\frac{3}{4}$,OM=OB.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c交x轴于点A、B,交y轴于点M,OA=3,tan∠AMO=$\frac{3}{4}$,OM=OB. 在等腰△ABC中,顶角∠A=100°,作∠B的平分线交AC于点E,求证:AE+BE=BC.
在等腰△ABC中,顶角∠A=100°,作∠B的平分线交AC于点E,求证:AE+BE=BC. 如图,点A,B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人同时从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的两倍,经过一段时间后,甲乙分别运动到点C,D,当乙机器人到达点B时,甲乙同时停止运动.
如图,点A,B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人同时从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的两倍,经过一段时间后,甲乙分别运动到点C,D,当乙机器人到达点B时,甲乙同时停止运动.