题目内容
6.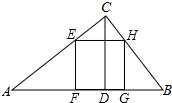 如图,在△ABC中,已知CD为边AB上的高,正方形EFGH的四个顶点分别在△ABC上,求证:$\frac{1}{AB}=\frac{1}{CD}=\frac{1}{EF}$.
如图,在△ABC中,已知CD为边AB上的高,正方形EFGH的四个顶点分别在△ABC上,求证:$\frac{1}{AB}=\frac{1}{CD}=\frac{1}{EF}$.
分析 根据正方形的性质得到EF⊥AB,证得EF∥CD,得到△AEF∽△ACD,根据相似三角形的性质得到$\frac{EF}{CD}=\frac{AE}{AC}$①,由△CEH∽△CAB,得到$\frac{EH}{AB}=\frac{CE}{AC}$,由于EH=EF,得到$\frac{EF}{AB}=\frac{CE}{AC}$②,①+②得$\frac{EF}{CD}+\frac{EF}{AB}=\frac{AE}{AC}+\frac{CE}{AC}$=1,即可得到结论.
解答  证明:∵四边形EFGH是正方形,
证明:∵四边形EFGH是正方形,
∴EF⊥AB,
∵CD⊥AB,
∴EF∥CD,
∴△AEF∽△ACD,
∴$\frac{EF}{CD}=\frac{AE}{AC}$①,
∵EH∥AB,
∴△CEH∽△CAB,
∴$\frac{EH}{AB}=\frac{CE}{AC}$,
∵EH=EF,
∴$\frac{EF}{AB}=\frac{CE}{AC}$②,
①+②得,$\frac{EF}{CD}+\frac{EF}{AB}=\frac{AE}{AC}+\frac{CE}{AC}$=1,
∴$\frac{1}{AB}+\frac{1}{CD}=\frac{1}{EF}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
18.下列选项中,能清楚地反映数据的个数变化情况的统计图是( )
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 直方图 |
15.下列命题不正确的是( )
| A. | 用四舍五入法对0.05049取近似值为0.050(精确到0.001) | |
| B. | 若代数式$\frac{x-2}{x+2}$有意义,则x的取值范围是x≠2且x≠-2 | |
| C. | 数据1,2,3,4的中位数是2.5 | |
| D. | 月球距离地球表面约为384000000米,将这个距离用科学记数法表示为3.84×108米 |
 如图,点A,B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人同时从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的两倍,经过一段时间后,甲乙分别运动到点C,D,当乙机器人到达点B时,甲乙同时停止运动.
如图,点A,B在以点O为圆心的圆上,且∠AOB=30°,如果甲机器人从点A出发沿着圆周按顺时针方向以每秒5°的速度行驶,乙机器人同时从点B出发沿着圆周按逆时针方向行驶,速度是甲机器人的两倍,经过一段时间后,甲乙分别运动到点C,D,当乙机器人到达点B时,甲乙同时停止运动. 四条直线AB,CD,EF,GH相交成如图所示的形状,那么与∠FPD构成同位角的角是∠HQD、∠FMB.
四条直线AB,CD,EF,GH相交成如图所示的形状,那么与∠FPD构成同位角的角是∠HQD、∠FMB.