题目内容
14.先化简(x+1-$\frac{15}{x-1}$)÷$\frac{{x}^{2}-8x+16}{1-x}$,根据自己的喜好选择一个你认为合适的x值代入求值.分析 先把括号里面的式子进行通分,再把除法转化成乘法,然后进行约分,最后找一个适当的值代入计算即可.
解答 解:(x+1-$\frac{15}{x-1}$)÷$\frac{{x}^{2}-8x+16}{1-x}$
=[$\frac{(x+1)(x-1)}{x-1}$-$\frac{15}{x-1}$]÷$\frac{{x}^{2}-8x+16}{1-x}$
=$\frac{(x+1)(x-1)-15}{x-1}$÷$\frac{(x-4)^{2}}{1-x}$
=$\frac{{x}^{2}-16}{x-1}$×$\frac{1-x}{(x-4)^{2}}$
=$\frac{(x+4)(x-4)}{x-1}$×$\frac{1-x}{(x-4)^{2}}$
=$\frac{x+4}{4-x}$,
当x=2时,原式=$\frac{2+4}{4-2}$=3.
点评 此题考查了分式的化简求值,用到的知识点是通分、约分、因式分解、平方差公式、完全平方公式;解答此题的关键是把分式化到最简,然后找一个合适的值代入.

练习册系列答案
相关题目
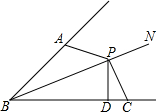 已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.
已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.
 如图,长方形ABCD中,AB=x2+4x+3,设长方形面积为S.
如图,长方形ABCD中,AB=x2+4x+3,设长方形面积为S. 如图,写出图中所有同位角、内错角、同旁内角.
如图,写出图中所有同位角、内错角、同旁内角.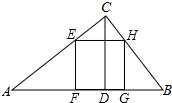 如图,在△ABC中,已知CD为边AB上的高,正方形EFGH的四个顶点分别在△ABC上,求证:$\frac{1}{AB}=\frac{1}{CD}=\frac{1}{EF}$.
如图,在△ABC中,已知CD为边AB上的高,正方形EFGH的四个顶点分别在△ABC上,求证:$\frac{1}{AB}=\frac{1}{CD}=\frac{1}{EF}$.