Question

如右图，△ABC的外接圆O半径为3，AB=2，AD为BC边上的高，则cos∠DAC=________．

Answer 1

分析：首先作直径AE，连接BE，根据圆周角定理，即可得∠ABE=90°，∠E=∠C，继而可证得∠BAE=∠DAC，然后在Rt△ABE中，利用三角函数的性质，即可求得答案．
解答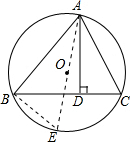：解：作直径AE，连接BE，
∴∠ABE=90°，∠E=∠C，
∵AD为BC边上的高，
∴∠ADC=90°，
∴∠ADC=∠ABE，
∴∠BAE=∠DAC，
∵△ABC的外接圆O半径为3，
∴AE=6，
在Rt△ABE中，cos∠BAE===．
∴cos∠DAC=．
故答案为：．
点评：此题考查了圆周角定理与三角函数的性质．此题难度适中，解题的关键是注意数形结合思想的应用，注意辅助线的作法．