题目内容
19. 老师在上概率课时,邀请小明和小华两名同学来做游戏,要求:小明用不透明的白布包住三根同样颜色、长短的细绳AA1、BB1、CC1,只露出它们的头和尾,(如图所示).
老师在上概率课时,邀请小明和小华两名同学来做游戏,要求:小明用不透明的白布包住三根同样颜色、长短的细绳AA1、BB1、CC1,只露出它们的头和尾,(如图所示).(1)小华从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
(2)小华先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,这三根绳子能连结成一根长绳就算小华赢,否则,就算小明赢.这个游戏公平吗?
分析 (1)直接根据概率公式求解;
(2)左右两端随机选两个打一个结各有三个情况:AB、AC、BC和A1B1、A1C1、B1C1,然后利用树状图展示所有9种等可能的结果数,找出三根绳子能连结成一根长绳的结果数,再计算小华赢和小明赢的概率,然后通过比较概率的大小判断游戏的公平性.
解答 解:(1)小华从这三根绳子中随机选一根,恰好选中绳子AA1的概率是=$\frac{1}{3}$;
(2)画树状图:
共有9种等可能的结果数,其中三根绳子能连结成一根长绳的结果数为6种,
所以小华赢的概率=$\frac{6}{9}$=$\frac{2}{3}$,则小明赢的概率=1-$\frac{2}{3}$=$\frac{1}{3}$,
因为$\frac{2}{3}$>$\frac{1}{3}$,
所以这个游戏不公平.
点评 本题考查了游戏公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.也考查了列表法与树状图.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
11. 如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
 如图,在正方形网格中,∠1、∠2、∠3的大小关系( )
如图,在正方形网格中,∠1、∠2、∠3的大小关系( )| A. | ∠1=∠2=∠3 | B. | ∠1<∠2<∠3 | C. | ∠1=∠2>∠3 | D. | ∠1<∠2=∠3 |
 如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D. 如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,PB=4,则cosP的值为$\frac{4}{5}$.
如图,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=8,PB=4,则cosP的值为$\frac{4}{5}$.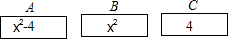 如图所示(背面完全相同)A、B、C三张卡片,正面分别写上整式x2-4,x2,4;现将这三张卡片背面向上洗匀,从中随机抽取两张,然后将所抽取卡片上的两个整式分别放在“=”的两边,组成一个等式.
如图所示(背面完全相同)A、B、C三张卡片,正面分别写上整式x2-4,x2,4;现将这三张卡片背面向上洗匀,从中随机抽取两张,然后将所抽取卡片上的两个整式分别放在“=”的两边,组成一个等式. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).请你根据图象回答下列问题.
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).请你根据图象回答下列问题.