题目内容
12.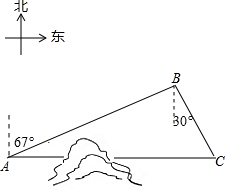 如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地.已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向.若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)(参考数据:sin67°≈$\frac{12}{13}$,cos67°≈$\frac{5}{13}$,tan67°≈$\frac{12}{5}$,$\sqrt{3}$≈1.73)
分析 过点B作BD⊥AC于点D,利用锐角三角函数的定义求出AD及CD的长,进而可得出结论.
解答 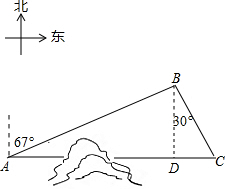 解:过点B作BD⊥AC于点D,
解:过点B作BD⊥AC于点D,
∵B地位于A地北偏东67°方向,距离A地520km,
∴∠ABD=67°,
∴AD=AB•sin67°=520×$\frac{12}{13}$=$\frac{6240}{13}$=480km,
BD=AB•cos67°=520×$\frac{5}{13}$=$\frac{2600}{13}$=200km.
∵C地位于B地南偏东30°方向,
∴∠CBD=30°,
∴CD=BD•tan30°=200×$\frac{\sqrt{3}}{3}$=$\frac{200\sqrt{3}}{3}$,
∴AC=AD+CD=480+$\frac{200\sqrt{3}}{3}$≈480+116=596(km).
答:A地到C地之间高铁线路的长为596km.
点评 本题考查的是解直角三角形的应用-方向角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
相关题目
3.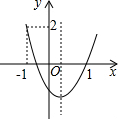 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
①abc<0;
②2a+b>0;
③a+c=1;
④a-b<2.
其中正确结论的有( )
 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:①abc<0;
②2a+b>0;
③a+c=1;
④a-b<2.
其中正确结论的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.2的绝对值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
2.在$\sqrt{3}$,$\frac{1}{2}$,0,-2这四个数中,为无理数的是( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
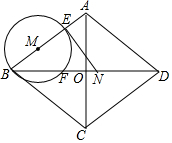 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.