题目内容
如 图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
( 1)求证:△BDE∽△BAC;
1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
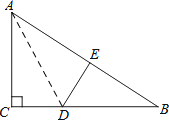
证明:(1)∵∠C=90°,△ACD沿AD折叠,
∴∠C=∠AED=90°,
∴∠DEB=∠C=90°,
∵∠B=∠B,
∴△BDE∽△BAC;
(2)由勾股定理得,AB=10.
由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C=90°.
∴BE=AB﹣AE=10﹣6=4,
在Rt△BDE中,由勾股定理得,
DE2+BE2=BD2,
即CD2+42=(8﹣CD)2,
解得:CD=3,
在Rt△ACD中,由勾股定理得AC2+CD2=AD2,
即32+62=AD2,
解得:AD= .
.

练习册系列答案
相关题目
 40000000毫升,将2540000000用科学记数法表示应为 。
40000000毫升,将2540000000用科学记数法表示应为 。
 .
. 的倒数是( )
的倒数是( )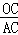 =
=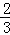 ,且OC=4,求PA的长和tanD的值.
,且OC=4,求PA的长和tanD的值.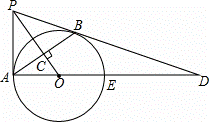
 +
+ =1.
=1.