题目内容
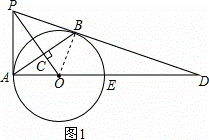
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若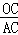 =
=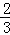 ,且OC=4,求PA的长和tanD的值.
,且OC=4,求PA的长和tanD的值.
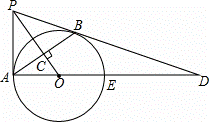
(1)证明:连接OB,则OA=OB,
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵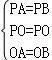 ,
,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切线;
(2)连接BE,

∵ =
= ,且OC=4,
,且OC=4,
∴AC=6,
∴ AB=12,
AB=12,
在Rt△ACO中,
由勾股定理得:AO= =2
=2 ,
,
∴AE=2OA=4 ,OB=OA=2
,OB=OA=2 ,
,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OC•PC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP=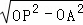 =3
=3 ,
,
∴PB=PA=3 ,
,
∵AC=BC,OA=OE,
∴OC=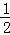 BE,OC∥BE,
BE,OC∥BE,
∴BE=2OC=8,BE∥OP,
∴△DBE∽△DPO,
∴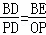 ,
,
即 ,
,
解得:BD= ,
,
在Rt△OBD中,
tanD=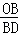 =
=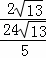 =
= .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
如图汽车标志中不是中心对称图形的是( )
|
| A. |
| B. |
| C. |
| D. |
|
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
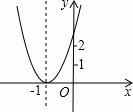
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )

|
| A. | 110° | B. | 80° | C. | 70° | D. | 60° |
 图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.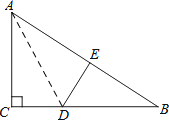

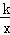 (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.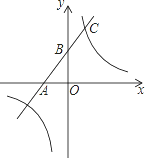




 )﹣2﹣2sin60°+
)﹣2﹣2sin60°+ .
.