题目内容
19.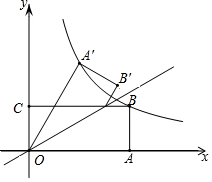 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.
如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.
分析 设B(m,1),得到OA=BC=m,根据轴对称的性质得到OA′=OA=m,∠A′OD=∠AOD=30°,求得∠A′OA=60°,过A′作A′E⊥OA于E,解直角三角形得到A′($\frac{1}{2}$m,$\frac{\sqrt{3}}{2}$m),列方程即可得到结论.
解答  解:∵四边形ABCO是矩形,AB=1,
解:∵四边形ABCO是矩形,AB=1,
∴设B(m,1),
∴OA=BC=m,
∵四边形OA′B′D与四边形OABD关于直线OD对称,
∴OA′=OA=m,∠A′OD=∠AOD=30°,
∴∠A′OA=60°,
过A′作A′E⊥OA于E,
∴OE=$\frac{1}{2}$m,A′E=$\frac{\sqrt{3}}{2}$m,
∴A′($\frac{1}{2}$m,$\frac{\sqrt{3}}{2}$m),
∵反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,
∴$\frac{1}{2}$m•$\frac{\sqrt{3}}{2}$m=m,
∴m=$\frac{4\sqrt{3}}{3}$,
∴k=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查了反比例函数图象上点的坐标特征,矩形的性质,轴对称的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
11.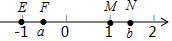 如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )
如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )
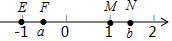 如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )
如图,实数-1,a,1,b在数轴上的对应点分别为E,F,M,N,这四个数中绝对值最小的数对应的点是( )| A. | 点E | B. | 点F | C. | 点M | D. | 点N |
8.“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京召开,“一带”指的是“丝绸之路经济带”,“一路”指的是“21”.“一带一路”沿线大多是新兴经济体和发展中国家,经济总量约210 000亿美元,将“210 000亿”用科学记数法表示应为( )
| A. | 21×104亿 | B. | 2.1×104亿 | C. | 2.1×105亿 | D. | 0.21×106亿 |
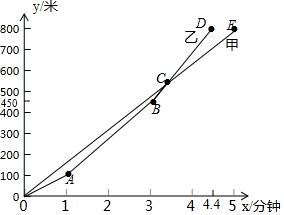 百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题:
百舸竞渡,激情飞扬.为纪念爱国诗人屈原,某市举行龙舟赛.甲、乙两支龙舟队在比赛时,路程y(米)与时间x(分钟)之间的函数图象如图所示,根据图象回答下列问题: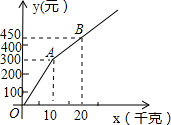 甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.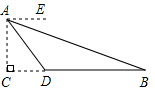 为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)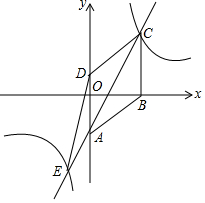 已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b.
已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b.