题目内容
1．已知x=$\frac{16}{\sqrt{17}+1}$，求x5+2x4-17x3-x2+18x-17的值．分析 根据x=$\frac{16}{\sqrt{17}+1}$=$\sqrt{17}$-1得到（x+1）2=17，化简得到：x2+2x=16，然后将代数式进行因式分解后层层代入即可．
解答 解：∵x=$\frac{16}{\sqrt{17}+1}$=$\sqrt{17}$-1，
∴（x+1）2=17，
化简得到：x2+2x=16，
∴x5+2x4-17x3-x2+18x-17
=x3（x2+2x）-17x3-x2+18x-17
=16x3-17x3-x2+18x-17
=-x3-x2+18x-17
=-x（x2+2x）+x2+18x-17
=x2+2x-17
=16-17
=-1．
点评 本题考查了二次根式的化简与因式分解的应用，解题的关键是对代数式进行正确的因式分解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．在平面直角坐标系中，点A在x轴上方，y轴左侧，距离每条坐标轴都是1个单位长度，则点A的坐标为（ ）
| A． | （1，1） | B． | （-1，-1） | C． | （-1，1） | D． | （1，-1） |
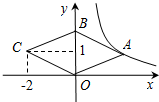如图，菱形OABC的顶点B在y轴上，顶点C的坐标为（-2，1），若反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点A，则k的值为（ ）