题目内容
6.解方程组:$\left\{\begin{array}{l}{x:6=y:5①}\\{x:2=z:3②}\\{x+y+z=40③}\end{array}\right.$.分析 利用①②,分别表示用x出y,z,进而求出x的值进而得出答案.
解答 解:由①得:y=$\frac{5}{6}$x,
由②得:z=$\frac{3}{2}$x,
则x+$\frac{5}{6}$x+$\frac{3}{2}$x=40,
解得x=12,
则y=$\frac{5}{6}$×12=10,
z=$\frac{3}{2}$×12=18.
故三元一次方程组的解为:$\left\{\begin{array}{l}{x=12}\\{y=10}\\{z=18}\end{array}\right.$.
点评 此题主要考查了三元一次方程组的解法,正确利用x表示出y,z的值是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
11. 如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( )
如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( )
 如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( )
如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( )| A. | 15° | B. | 30° | C. | 75° | D. | 150° |
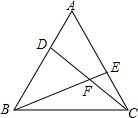 如图,点D、E分别在等边△ABC的AB、AC边上,BE与CD交于F,∠BFC=120°,求证:AD=CE.
如图,点D、E分别在等边△ABC的AB、AC边上,BE与CD交于F,∠BFC=120°,求证:AD=CE. 经调查,某班学生上学所用的交通工具中,自行车占$\frac{1}{2}$,公交车占$\frac{1}{3}$,其他占$\frac{1}{6}$,请画出扇形统计图描述以上统计数据.
经调查,某班学生上学所用的交通工具中,自行车占$\frac{1}{2}$,公交车占$\frac{1}{3}$,其他占$\frac{1}{6}$,请画出扇形统计图描述以上统计数据.