题目内容
2.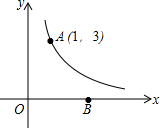 如图,反比例函数y=$\frac{k-5}{x}$(k为常数,且k≠5)经过点A(1,3).
如图,反比例函数y=$\frac{k-5}{x}$(k为常数,且k≠5)经过点A(1,3).(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.
分析 (1)利用待定系数法把A(1,3)代入反比例函数y=$\frac{k-5}{x}$可得k的值,进而得到解析式;
(2)根据△AOB的面积为6求出B点坐标,再设直线AB的解析式为y=mx+b,把A、B两点代入可得m、b的值,进而得到答案.
解答 解:(1)∵反比例函数y=$\frac{k-5}{x}$(k为常数,且k≠5)经过点A(1,3),
∴3=$\frac{k-5}{1}$,解得:k=8,
∴反比例函数解析式为y=$\frac{8-5}{x}$=$\frac{3}{x}$;
(2)设B(a,0),则BO=a,
∵△AOB的面积为6,
∴$\frac{1}{2}$a×3=6,解得:a=4,
∴B(4,0).
设直线AB的解析式为y=mx+b,
∵直线经过A(1,3),B(4,0),
∴$\left\{\begin{array}{l}{m+b=3}\\{4m+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为y=-x+4.
点评 此题主要考查了待定系数法求一次函数解析式和反比例函数解析式,关键是正确求出B点坐标.

练习册系列答案
相关题目
13.如图图形中既是轴对称又是中心对称的图形是( )
| A. |  | B. |  | C. |  | D. |  |
10.为进一步普及环保和健康知识,我市某校举行了“美丽德州,环保德州”的知识竞赛,某班的学生成绩统计如下:
则该班学生成绩的众数和中位数分别是( )
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A. | 90分,80分 | B. | 80分,90分 | C. | 80分,80分 | D. | 70分,80分 |
17.下列运算正确的是( )
| A. | 2x2+x=3x3 | B. | (-x)3+x2=-x6 | C. | (2x2)3=6x6 | D. | (-x)2÷x=x |
7.函数y=-x2+2x+2的顶点坐标是( )
| A. | (1,3) | B. | (-1,3) | C. | (1,-2) | D. | (-1,2) |