题目内容
11. 如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )| A. | (11-2$\sqrt{2}$)米 | B. | (11$\sqrt{3}$-2$\sqrt{2}$)米 | C. | (11-2$\sqrt{3}$)米 | D. | (11$\sqrt{3}$-4)米 |
分析 出现有直角的四边形时,应构造相应的直角三角形,利用相似求得PB、PC,再相减即可求得BC长.
解答 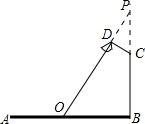 解:如图,延长OD,BC交于点P.
解:如图,延长OD,BC交于点P.
∵∠ODC=∠B=90°,∠P=30°,OB=11米,CD=2米,
∴在直角△CPD中,DP=DC•cot30°=2$\sqrt{3}$m,PC=CD÷(sin30°)=4米,
∵∠P=∠P,∠PDC=∠B=90°,
∴△PDC∽△PBO,
∴$\frac{PD}{PB}$=$\frac{CD}{OB}$,
∴PB=$\frac{PD•OB}{CD}$=$\frac{2\sqrt{3}×11}{2}$=11$\sqrt{3}$米,
∴BC=PB-PC=(11$\sqrt{3}$-4)米.
故选:D.
点评 本题通过构造相似三角形,综合考查了相似三角形的性质,直角三角形的性质,锐角三角函数的概念.

练习册系列答案
相关题目
2. 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )
 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
19.下列命题正确的是( )
| A. | 矩形的对角线互相垂直 | |
| B. | 两边和一角对应相等的两个三角形全等 | |
| C. | 分式方程$\frac{x-2}{2x-1}$+1=$\frac{1.5}{1-2x}$可化为一元一次方程x-2+(2x-1)=-1.5 | |
| D. | 多项式t2-16+3t因式分解为(t+4)(t-4)+3t |
16.一组数据6、4、a、3、2的平均数是4,则这组数据的方差为( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 10 |
3. 如图,OA⊥OB,∠1=35°,则∠2的度数是( )
如图,OA⊥OB,∠1=35°,则∠2的度数是( )
 如图,OA⊥OB,∠1=35°,则∠2的度数是( )
如图,OA⊥OB,∠1=35°,则∠2的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 70° |
20.下列因式分解正确的是( )
| A. | a4b-6a3b+9a2b=a2b(a2-6a+9) | B. | x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2 | ||
| C. | x2-2x+4=(x-2)2 | D. | 4x2-y2=(4x+y)(4x-y) |
5.在解方程:$\frac{x+1}{2}-\frac{x-1}{3}=1$时,去分母正确的是( )
| A. | 3x+1-2x-1=1 | B. | 3x+1-2X-1=6 | C. | 3(x+1)-2(x-1)-=1 | D. | 3(x+1)-2(x-1)=6 |

 兴的实际距离约为80km.
兴的实际距离约为80km.