Question

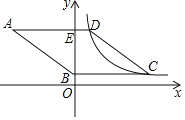
【题目】如图，抛物线y＝ax2+bx﹣2交x轴负半轴于点A（﹣1，0），与y轴交于B点．过B点的直线l交抛物线于点C（3，﹣1）．过点C作CD⊥x轴，垂足为D．点P为x轴正半轴上的动点，过P点作x轴的垂线，交直线l于点E，交抛物线于点F．设P点的横坐标为t．

（1）求抛物线的解析式；

（2）连接OE，求△POE面积的最大值；

（3）连接DE，CF，是否存在这样的t值：以点C，D，E，F为顶点的四边形是平行四边形？请说明理由．

Answer 1

【答案】（1）；（2）；（3）存在这样的t值：以点C，D，E，F为顶点的四边形是平行四边形．

【解析】

1）将点A、C的坐标代入函数解析式，利用解方程组求得系数的值即可；

（2）根据三角形的面积公式，函数图象上点的坐标特征求得S△POE=t（t-2）=（t-3）2-，所以由二次函数的性质求得答案；

（3）根据平行四边形的对边相等的性质和坐标与图形的性质求得答案．

（1）把A（﹣1，0），C（3，﹣1）代入y＝ax2+bx﹣2，得

．

解得．

则该抛物线的解析式为；

（2）由（1）知，抛物线的解析式为，则B（0，﹣2）．

设直线BC的解析式为：y＝kx+d（k≠0）．

把B（0，﹣2）、C（3，﹣1）代入，得．

解得．

故直线BC的解析式为 ．

∴E（t，t﹣2）

∴S△POE＝t（t-2）=（t-3）2-．

∴△POE面积的最大值是；

（3）存在这样的t值．

理由：E（t，），F（t，）．

若以点C，D，E，F为顶点的四边形是平行四边形，则EF＝CD＝1，

即﹣（）﹣（2﹣t）＝1．

整理得：7t2﹣21t+12＝0．

∵△＝（﹣21）2﹣4×7×12＞0，

∴方程7t2﹣21t+12＝0有解．

∴存在这样的t值：以点C，D，E，F为顶点的四边形是平行四边形．