题目内容
4.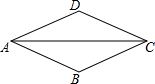 如图,在?ABCD中,AC平分∠DAB,AB=7,则?ABCD的周长为28.
如图,在?ABCD中,AC平分∠DAB,AB=7,则?ABCD的周长为28.
分析 首先证得△ADC≌△ABC,由全等三角形的性质易得AD=AB,由菱形的判定定理得?ABCD为菱形,由菱形的性质得其周长.
解答 解:∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵四边形ABCD为平行四边形,
∴∠B=∠D,
在△ADC和△ABC中,
$\left\{\begin{array}{l}{∠B=∠D}\\{∠BAC=∠DAC}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△ABC,
∴AD=AB,
∴四边形ABCD为菱形,
∴AD=AB=BC=CD=7,
?ABCD的周长为:7×4=28,
故答案为:28.
点评 本题主要考查了全等三角形的判定及菱形的判定及性质,找出判定菱形的条件是解答此题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
14.二次根式$\sqrt{a+1}$中,字母a的取值范围为( )
| A. | a≥-1 | B. | a≥0 | C. | a≥1 | D. | a≤-1 |
13.选择用反证法证明“已知:∠A,∠B,∠C是△ABC的三个内角,求证:∠A,∠B,∠C三个内角中至少有一个角大于或等于60°”时,应先假设( )
| A. | ∠A>60°,∠B>60°,∠C>60° | B. | ∠A≥60°,∠B≥60°,∠C≥60° | ||
| C. | ∠A<60°,∠B<60°,∠C<60° | D. | ∠A≤60°,∠B≤60°,∠C≤60° |
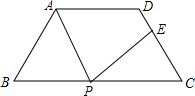 如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.
如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.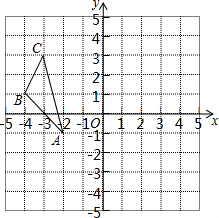 如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-2,-1),B(-4,1),C(-3,3).△ABC关于原点O对称的图形是△A1B1C1.
如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-2,-1),B(-4,1),C(-3,3).△ABC关于原点O对称的图形是△A1B1C1.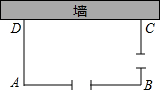 矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的校门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少.
矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的校门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少.