题目内容
19.比较大小:3$\sqrt{2}$>2$\sqrt{3}$,$\root{3}{7}$<2.分析 先运用二次根式的性质把根号外的因数移到根号内,然后比较被开方数的大小即可得出3$\sqrt{2}$>2$\sqrt{3}$;由2=$\root{3}{8}$,即可得出$\root{3}{7}$<2.
解答 解:∵3$\sqrt{2}$=$\sqrt{18}$,2$\sqrt{3}$=$\sqrt{12}$,
∴3$\sqrt{2}$>2$\sqrt{3}$;
∵2=$\root{3}{8}$,
∴$\root{3}{7}$<2.
故答案为>,<.
点评 此题主要考查了实数的大小的比较,掌握比较两个无理数的大小的方法:把根号外的因数移到根号内,只需比较被开方数的大小.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.若x等于它的倒数,则$\frac{(x-3)(x+2)}{{x}^{2}-9}$•$\frac{(x-3)(x-2)}{{x}^{2}-4}$的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2或-2 | D. | -2或-$\frac{1}{2}$ |
8.下列各式计算正确的有( )
| A. | (p5q4)÷(2p3q)=2p2q3 | B. | (-a+5)(-a-5)=-a2-25 | ||
| C. | $\frac{1}{a}+\frac{2}{a}=\frac{3}{2a}$ | D. | $\frac{2a}{{{a^2}-4}}-\frac{1}{a-2}=\frac{1}{a+2}$ |
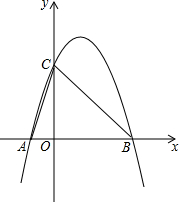 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则: