Question

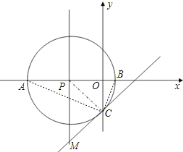
【题目】如图，在平面直角坐标系中，为原点，点坐标为，点坐标为，以为直径的圆与轴的负半轴交于点．

（1）求图象经过，，三点的抛物线的解析式；

（2）设点为所求抛物线的顶点，试判断直线与的关系，并说明理由．

Answer 1

【答案】（1）（2）直线与相切，理由见解析

【解析】

（1）已知A、B两点的坐标，要求抛物线的解析式，即要求点C的坐标，由相似三角形的判定与性质求出OC的长度，即可求出点C的坐标；（2）根据抛物线解析式求出点M的坐标，分别求出MP、CP、CM的长度，利用勾股定理逆定理判定△CPM为直角三角形，从而得出PC⊥MC，所以直线MC与⊙P相切.

解：（1）连接AC、BC；

∵AB是⊙P的直径，

∴∠ACB=90°，即∠ACO+∠BCO=90°，

∵∠BCO+∠CBO=90°，

∴∠CBO=∠ACO，

∵∠AOC=∠BOC=90°，

∴△AOC∽△COB，

∴=，

∴OC2=OA·OB=16，

∴OC=4，

故C(0，﹣4)，

设抛物线的解析式为：y=a(x+8)(x﹣2)，

代入C点坐标得：a(0+8)(0﹣2)=﹣4，a=，

故抛物线的解析式为：y=(x+8)(x﹣2)=+x﹣4；

(2)由(1)知：y=+x﹣4=﹣；

则M(﹣3，﹣)，

又∵C(0，﹣4)，P(﹣3，0)，

∴MP=，PC=5，MC=，

∴MP2=MC2+PC2，即△MPC是直角三角形，且∠PCM=90°，

故直线MC与⊙P相切．