Question

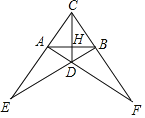
【题目】如图，线段CD垂直平分线段AB，垂足为H，CA的延长线交BD的延长线于E，CB的延长线交AD的延长线于F．

（1）求证：DE＝DF；

（2）若AE＝AB，∠E＝22.5°，则直接写出图中内角含有45°等腰三角形（写出3个即可）．

Answer 1

【答案】（1）证明见解析；（2）△ACH，△BCH，△CAB都是含45°角的等腰三角形，理由见解析.

【解析】

（1）根据线段垂直平分线得出AC＝BC，BD＝AD，推出∠CBE＝∠CAF，证△BCE≌△ACF，推出BE＝AF，即可得出答案；

（2）根据全等三角形的性质和垂直的定义即可得到结论．

（1）证明：∵线段CD垂直平分AB，

∴AC＝BC，AD＝BD，

∴∠CAB＝∠CBA，∠BAD＝∠ABD，

∴∠CAB+∠BAD＝∠CBA+∠ABD，

即∠CBE＝∠CAF，

在△BCE和△ACF中

∵，

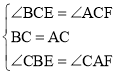∴△BCE≌△ACF（ASA），

∴BE＝AF，

∵BD＝AD，

∴BE﹣BD＝AF﹣AD，

即DE＝DF；

（2）解：△ACH，△BCH，△CAB都是含45°角的等腰三角形，

理由：由（1）证得△BCE≌△ACF，

∴CE＝CF，

∴AE＝BF，

∵AB＝AE，

∴AB＝BF，

∴∠E＝∠ABE＝∠BAF＝∠F＝22.5°，

∴∠CAB＝∠CBA＝45°，

∵CD⊥AB，

∴∠AHC＝∠BHC＝90°，

∴∠ACH＝∠BCH＝45°．

即：△ACH，△BCH，△CAB都是含45°角的等腰三角形