题目内容
15.若方程mx+13=4x+11的解为负数,则m的取值范围是m>4.分析 解关于x的方程得x=$\frac{2}{4-m}$,由方程的解为负数得到关于m的不等式,解不等式即可.
解答 解:解方程mx+13=4x+11得:x=$\frac{2}{4-m}$,
∵方程的解为负数,
∴$\frac{2}{4-m}$<0,即4-m<0,
解得:m>4,
故答案为:m>4.
点评 本题主要考查解一元一次方程和不等式的能力,根据题意得出关于m的不等式是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
5.定义:我们把关于x的一元二次方程ax2+bx+c=0与cx2+bx+a=0(ac≠0,a≠c)称为一元二次方程的一对“和谐方程”.
(1)正确填写表格中的空白.
(2)根据表1,猜想原方程的两根与“和谐方程”的两根之间关系,并证明.
(3)已知关于x的方程2016x2+bx-1=0的两根是x1=-1,x2=$\frac{1}{2016}$.请利用(2)中的结论,解关于x的方程:(x-1)2-bx+b=2016.
(1)正确填写表格中的空白.
| 原方程 | 原方程的根 | ”和谐方程“ | ”和谐方程“的根 |
| x2+6x+9=0 | x1=-3,x2=-3 | 9x2+6x+1=0 | x1=-$\frac{1}{3}$,x2=-$\frac{1}{3}$ |
| x2-5x+6=0 | x1=2,x2=3 | 6x2-5x+1=0 | x1=$\frac{1}{2}$,x2=$\frac{1}{3}$ |
| -$\frac{1}{6}$x2-$\frac{1}{6}$x+1=0 | x1=2,x2=-3 | x2-$\frac{1}{6}$x-$\frac{1}{6}$=0 | x1=$\frac{1}{2}$,x2=-$\frac{1}{3}$ |
| 2x2-3x-2=0 | x1=2,x2=-$\frac{1}{2}$ | -2x2-3x+2=0 | x1=$\frac{1}{2}$,x2=-2 |
(3)已知关于x的方程2016x2+bx-1=0的两根是x1=-1,x2=$\frac{1}{2016}$.请利用(2)中的结论,解关于x的方程:(x-1)2-bx+b=2016.
 时,原方程应变形为( )
时,原方程应变形为( ) B.
B.  C.
C.  D.
D. 

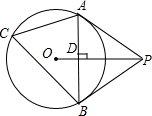 如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D.
如图,已知△ABC内接于⊙O,P是圆外一点,PA为⊙O的切线,且PA=PB,连接OP,线段AB与线段OP相交于点D. 如图,已知l1∥l2,∠A=40°,∠1=60°,求∠2的度数.
如图,已知l1∥l2,∠A=40°,∠1=60°,求∠2的度数.