题目内容
 如图,点E在?ABCD的边BC延长线上,且BC=CE,∠ADB=∠E.
如图,点E在?ABCD的边BC延长线上,且BC=CE,∠ADB=∠E.试说明四边形ABCD是矩形.
分析:首先证明∠E=∠DBC,根据等角对等边可得DB=DE,进而得到△DBE是等腰三角形,再根据等腰三角形三线合一的性质可得DC⊥EB,进而得到∠DCB=90°,再根据有一个角是直角的平行四边形是矩形得到结论.
解答:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBE,
∵∠ADB=∠E,
∴∠E=∠DBC,
∴DB=DE,
∴△DBE是等腰三角形,
∵BC=CE,
∴DC⊥EB,
∴∠DCB=90°,
又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
∴AD∥BC,
∴∠ADB=∠DBE,
∵∠ADB=∠E,
∴∠E=∠DBC,
∴DB=DE,
∴△DBE是等腰三角形,
∵BC=CE,
∴DC⊥EB,
∴∠DCB=90°,
又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
点评:此题主要考查了矩形的判定,关键是证明DC⊥EB,掌握矩形的判定定理.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 25、如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.
25、如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.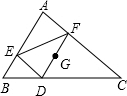 AC于点F.又知BC=5.
AC于点F.又知BC=5. 10、已知:如图,点D在△ABC的边BC上,DE∥AC交AB于E,DF∥AB交AC于F.
10、已知:如图,点D在△ABC的边BC上,DE∥AC交AB于E,DF∥AB交AC于F.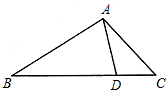 如图,点D在△ABC边BC上,且∠ADC=∠BAC,若AC=x,CD=x-2,BD=2x-2,则x的值是
如图,点D在△ABC边BC上,且∠ADC=∠BAC,若AC=x,CD=x-2,BD=2x-2,则x的值是 如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.