题目内容
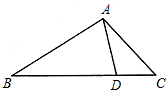如图，点D在△ABC边BC上，且∠ADC=∠BAC，若AC=x，CD=x-2，BD=2x-2，则x的值是分析：根据相似三角形的性质可证：△ABC∽△DAC，从而得到：
=
，将AC=x，CD=x-2，BD=2x-2代入其中，解得：x=4．
| AC |
| CD |
| BC |
| AC |
解答：解：∵∠ADC=∠BAC，∠C=∠C，
∴△ABC∽△DAC，
∴
=
，
即
=
，
解得：x=4或1（经检验，1不符合题意，舍去）
∴x=4．
故选B．
∴△ABC∽△DAC，
∴
| AC |
| CD |
| BC |
| AC |
即
| x |
| x-2 |
| x+2+2x-2 |
| x |
解得：x=4或1（经检验，1不符合题意，舍去）
∴x=4．
故选B．
点评：本题考查相似三角形的判定与性质，根据相似三角形对应边的比相等，转化为解方程的问题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
25、如图，点E在△ABC外部，点D在边BC上，DE交AC于F．若∠1=∠2=∠3，AC=AE，请说明△ABC≌△ADE的道理．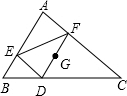
AC于点F．又知BC=5．
10、已知：如图，点D在△ABC的边BC上，DE∥AC交AB于E，DF∥AB交AC于F．
如图，点D在△ABC的边BC上，DC=AC=BD，∠ACB的平分线CF交AD于F，点E是AB的中点，连接EF．