题目内容
17．在正方形ABCD所在的平面内找一点P，使其与正方形中的每一边所构成的三角形均为等腰三角形，这样的点有5个．分析 作正方形与边平行的两条对称轴，两对称轴的交点为P点，然后分别以正方形的各边向外作等边三角形，则第三个顶点为P点．
解答 解：如图，满足条件的P点有5个．
∁
故答案为5．
点评 本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；两条对角线将正方形分成四个全等的等腰直角三角形，同时，正方形又是轴对称图形，有四条对称轴．
练习册系列答案
阅读快车系列答案
相关题目
8．
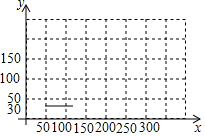某电信公司提供的移动通讯服务的收费标准有两种方案，如表所示：
设每月通话时间为x分，A，B两种方案每月话费分别为y1元，y2元．
（1）分别写出当x＞120时，y1关于x的函数表达式和当x＞200时，y2关于x的函数表达式；
（2）在如图所示的平面直角坐标系中，把y1和y2这两个函数图象的其余部分补画出来；（实线为A方案，虚线为B方案）
（3）结合图象考虑，若以节省费用的角度考虑，则应如何选择最优方案？
某电信公司提供的移动通讯服务的收费标准有两种方案，如表所示：| A方案 | B方案 | |
| 每月基本服务费 | 30元 | 50元 |
| 每月免费通话时间 | 120分 | 200分 |
| 超出后每分钟收费 | 0.4元 | 0.4元 |
（1）分别写出当x＞120时，y1关于x的函数表达式和当x＞200时，y2关于x的函数表达式；
（2）在如图所示的平面直角坐标系中，把y1和y2这两个函数图象的其余部分补画出来；（实线为A方案，虚线为B方案）
（3）结合图象考虑，若以节省费用的角度考虑，则应如何选择最优方案？
如图，点E，F在BC上，BE=CF，∠AFE=∠DEF，∠B=∠C，求证：AB=DC．
如图所示，已知等边△ABC中，AB=AC=BC，∠CAB=∠CBA=∠C=60°，BD=CE，AD与BE相交于点P，则∠APE=60°．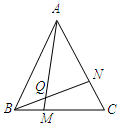
（1）学完全等三角形以后，老师布置了这样一道题：如图，点M、N分别在等边△ABC的BC、CA边上，且BM=CN，AM、BN交于点Q．求证：∠BQM=60°．（注意：等边三角形三条边都相等，每个内角都是60°）
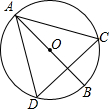如图，AB为⊙O的直径，点D在⊙O上，∠BAC=35°，则∠ADC=55°．