题目内容
10.(1)计算:-(2-$\sqrt{3}$)-(π-3.14)0+(1-cos30°)×($\frac{1}{2}$)-2;(2)先化简,再求值:$\frac{1}{a+1}$-$\frac{a+1}{{{a^2}-2a+1}}$÷$\frac{a+1}{a-1}$,其中a=$\sqrt{2}$.
分析 (1)根据去括号得法则、零指数幂、特殊角的三角函数值、负整数指数幂可以解答本题;
(2)根据分式的除法和减法可以化简题目中的式子,然后将a的值代入即可解答本题.
解答 解:(1)-(2-$\sqrt{3}$)-(π-3.14)0+(1-cos30°)×($\frac{1}{2}$)-2
=$\sqrt{3}$-2-1+(1-$\frac{\sqrt{3}}{2}$)×4
=$\sqrt{3}-2-1+4-2\sqrt{3}$
=$-\sqrt{3}+1$;
(2)$\frac{1}{a+1}$-$\frac{a+1}{{{a^2}-2a+1}}$÷$\frac{a+1}{a-1}$
=$\frac{1}{a+1}-\frac{a+1}{(a-1)^{2}}•\frac{a-1}{a+1}$
=$\frac{1}{a+1}-\frac{1}{a-1}$
=$\frac{a-1-(a+1)}{(a+1)(a-1)}$
=$\frac{-2}{{a}^{2}-1}$,
当a=$\sqrt{2}$时,原式=$\frac{-2}{(\sqrt{2})^{2}-1}=\frac{-2}{2-1}=-2$.
点评 本题考查分式的化简求值、去括号得法则、零指数幂、特殊角的三角函数值、负整数指数幂,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
20.矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
| A. | y=x2+8x+14 | B. | y=x2-8x+14 | C. | y=x2+4x+3 | D. | y=x2-4x+3 |
18.-3的绝对值是( )
| A. | -3 | B. | 3 | C. | ±3 | D. | $\frac{1}{3}$ |
15.肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )
| A. | 7.1×107 | B. | 0.71×10-6 | C. | 7.1×10-7 | D. | 71×10-8 |
19.若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y=-$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y2<y1<y3 |
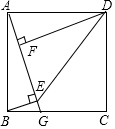 如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE. 反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b(k≠0)的图象的图象大致是( )
反比例函数y=$\frac{kb}{x}$的图象如图所示,则一次函数y=kx+b(k≠0)的图象的图象大致是( )






