��Ŀ����
17�� ��1����ƽ��ֱ������ϵ�У���A�������ǣ�0��2������x������ȡһ��M�����������ͼ���裺
��1����ƽ��ֱ������ϵ�У���A�������ǣ�0��2������x������ȡһ��M�����������ͼ���裺������AM�����߶�AM�Ĵ�ֱƽ����l1����M��x��Ĵ���l2����l1��l2�Ľ���ΪP��
����x���϶�θı��M��λ�ã��âٵķ����õ���Ӧ�ĵ�P������Щ����ƽ������������������
�۲컭��������L��������������ѧ�����������ߣ�
��2����������L������һ��P���߶�PA��PM��ʲô��ϵ�����P������Ϊ��x��y����������PA��PM�Ĺ�ϵ�õ�x��y����Ĺ�ϵʽ�������ɴ�ȷ������L��������������ó��Ľ����루1������IJ���һ����
���� ��1���������⣬��ȡ����M�㻭��ͼ�μ��ɣ�
��2������AP������A��AN��PM�������߶δ�ֱƽ���ߵ����ʵó�AP=PM=y�����ɹ��ɶ������ɵó����ۣ�
���  �⣺��1����ͼ��ʾ������L�������ߣ�
�⣺��1����ͼ��ʾ������L�������ߣ�
��2������AP������A��AN��PM��
��l1���߶�AM�Ĵ�ֱƽ���ߣ�P��l1�ϣ�
��PA=PM=y��
��PM��x�ᣬ
��AN=x��P��x��y����PN=y-2��
��AN2+PN2=AP2��
��x2+��y-2��2=y2��
��y=$\frac{1}{4}{x}^{2}$+1��
������L���������������ߣ�
���� ������Ҫ�����˸�����ͼ���Լ����ɶ����������������������ߣ������ֱ���������ǽ�����Ĺؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
7��������y=-��x-1��2-2�Ķ��������ǣ�������
| A�� | ��1��2�� | B�� | ��1��-2�� | C�� | ��-1��2�� | D�� | ��-1��-2�� |
2��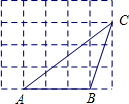 ��ͼ����5��4�ľ��������У�ÿ��С�����εı߳�����1������ABC������������ͼ����Ӧ�ĸ���ϣ���sinA��ֵΪ��������
��ͼ����5��4�ľ��������У�ÿ��С�����εı߳�����1������ABC������������ͼ����Ӧ�ĸ���ϣ���sinA��ֵΪ��������
 ��ͼ����5��4�ľ��������У�ÿ��С�����εı߳�����1������ABC������������ͼ����Ӧ�ĸ���ϣ���sinA��ֵΪ��������
��ͼ����5��4�ľ��������У�ÿ��С�����εı߳�����1������ABC������������ͼ����Ӧ�ĸ���ϣ���sinA��ֵΪ��������| A�� | 1 | B�� | $\frac{3}{4}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{4}{5}$ |
6�����и�ʽ$\frac{1}{5}$��1-x��=0��$\frac{{4{x^2}}}{��-3}$=0��$\frac{{{x^2}-{y^2}}}{2}$=0��$\frac{1}{x}+x=0$��x2+3x=0������һԪ���η��̵ĸ���Ϊ��������
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
7��������-3�����ǣ�������
| A�� | -3 | B�� | 3 | C�� | $\frac{1}{3}$ | D�� | $-\frac{1}{3}$ |
 ��ͼ��AB�ǡ�O���ң�CD�ǡ�O��ֱ����CD��AB������ΪE��CE=1��ED=3��
��ͼ��AB�ǡ�O���ң�CD�ǡ�O��ֱ����CD��AB������ΪE��CE=1��ED=3�� ��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��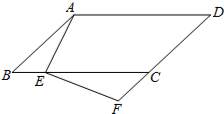 ��ͼ����?ABCD�У���E��BC���ϣ���F��DC���ӳ����ϣ��ҡ�DAE=��F����֤��BE•EC=FC•CD��
��ͼ����?ABCD�У���E��BC���ϣ���F��DC���ӳ����ϣ��ҡ�DAE=��F����֤��BE•EC=FC•CD��