题目内容
1.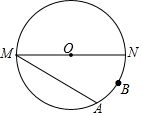 如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.
如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为$\widehat{AN}$的中点,P是直径MN上一动点.(1)利用尺规作图,确定当PA+PB最小时P点的位置(不写作法,但要保留作图痕迹).
(2)求PA+PB的最小值.
分析 (1)作点A关于MN的对称点A′,连接A′B,与MN的交点即为点P;
(2)由(1)可知,PA+PB的最小值即为A′B的长,连接OA′、OB、OA,先求∠A′OB=∠A′ON+∠BON=60°+30°=90°,再根据勾股定理即可得出答案.
解答 解:(1)如图1所示,点P即为所求;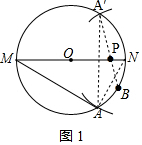
(2)由(1)可知,PA+PB的最小值即为A′B的长,连接OA′、OB、OA,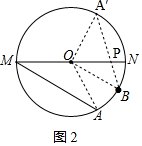
∵A′点为点A关直线MN的对称点,∠AMN=30°,
∴∠AON=∠A′ON=2∠AMN=2×30°=60°,
又∵B为$\widehat{AN}$的中点,
∴$\widehat{AB}$=$\widehat{BN}$,
∴∠BON=∠AOB=$\frac{1}{2}$∠AON=$\frac{1}{2}$×60°=30°,
∴∠A′OB=∠A′ON+∠BON=60°+30°=90°,
又∵MN=4,
∴OA′=OB=$\frac{1}{2}$MN=$\frac{1}{2}$×4=2,
∴Rt△A′OB中,A′B=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,即PA+PB的最小值为2$\sqrt{2}$.
点评 本题主要考查作图-复杂作图及轴对称的最短路线问题,熟练掌握轴对称的性质和圆周角定理、圆心角定理是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
12.某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
| 时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
| 售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
| 销量(斤) | 80-3x | 120-x | |
| 储存和损耗费用(元) | 40+3x | 3x2-64x+400 | |
16.某商店分两次购进 A、B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
| 购进数量(件) | 购进所需费用(元) | ||
| A | B | ||
| 第一次 | 30 | 40 | 3800 |
| 第二次 | 40 | 30 | 3200 |
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
6.10名初中毕业生的中招体育加试成绩(单位:分)统计如表:
则这组数据的平均数和中位数分别为( )
| 成绩/分 | 66 | 67 | 68 | 69 | 70 |
| 人数 | 1 | 4 | 1 | 2 | 2 |
| A. | 67,67.5 | B. | 68,68 | C. | 68,67.5 | D. | 67.5,68 |
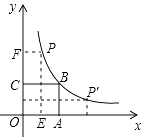 如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=$\frac{k}{x}$(k>0,x>0)的图象上点P(m,n)是函数图象上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.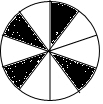 如图所示的圆形纸板被等分成10个扇形挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{2}{5}$.
如图所示的圆形纸板被等分成10个扇形挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{2}{5}$.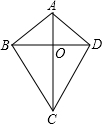 如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中: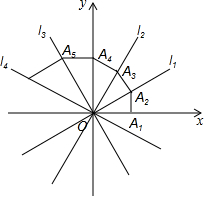 如图,四条直线l1:y1=$\frac{\sqrt{3}}{3}$x,l2:y2=$\sqrt{3}$x,l3:y3=-$\sqrt{3}$x,l4:y4=-$\frac{\sqrt{3}}{3}$x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为(($\frac{2\sqrt{3}}{3}$)2016,0).
如图,四条直线l1:y1=$\frac{\sqrt{3}}{3}$x,l2:y2=$\sqrt{3}$x,l3:y3=-$\sqrt{3}$x,l4:y4=-$\frac{\sqrt{3}}{3}$x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为(($\frac{2\sqrt{3}}{3}$)2016,0).