题目内容
设a是不等于1的有理数,我们把
称为a的差倒数,如:2的差倒数是
=-1,-1的差倒数是
=
.已知一列数:a1,a2,a3…a2015,从第2个数a2起每一个都是它前一个的差倒数,且a1=
,则a2015= .
| 1 |
| 1-a |
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 |
| 3 |
考点:规律型:数字的变化类
专题:
分析:根据差倒数的定义分别求出前几个数便不难发现,每3个数为一个循环组依次循环,用2015除以3,根据余数的情况确定出与a2015相同的数即可得解.
解答:解:∵a1=
,
a2=
=
,
a3=
=-2,
a4=
=
=a1,
…
∴这一列数3个3个的循环.
∵2015÷3=671…2
∴a2015=a2=
.
故答案为:
.
| 1 |
| 3 |
a2=
| 1 | ||
1-
|
| 3 |
| 2 |
a3=
| 1 | ||
1-
|
a4=
| 1 |
| 1-(-2) |
| 1 |
| 3 |
…
∴这一列数3个3个的循环.
∵2015÷3=671…2
∴a2015=a2=
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本此题考数字的变化规律,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,设点P到原点O的距离为p,OP与x轴正方向的夹角为a,则用[p,α]表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为[
,45°].若点Q的极坐标为[2,60°],则点Q的坐标为( )
| 2 |
A、(1,
| ||
B、(1,-
| ||
C、(
| ||
| D、(1,1) |
已知:1-(3m-5)2有最大值,则方程5m-4=3x+2的解是( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 已知:如图△ABC中,D、E、F分别是AB、AC、BC的中点.
已知:如图△ABC中,D、E、F分别是AB、AC、BC的中点.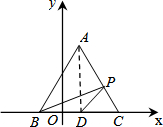 如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2
如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2