题目内容
(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲、乙走的路程图改成图2,两人走的路程远近相同吗?

(2)如果甲、乙走的路程图改成图2,两人走的路程远近相同吗?

考点:圆的认识
专题:计算题
分析:(1)甲所走的路径长为以AB为直径的半圆长,乙所走的路径长为以AC和BC为直径的两个半圆长的和,然后根据圆的周长公式进行计算,再比较大小;
(2)甲所走的路径长为以AB为直径的半圆长,乙所走的路径长为以AC、CD和DB为直径的三个半圆长的和,然后根据圆的周长公式分别计算他们所走的路径,再比较大小即可.
(2)甲所走的路径长为以AB为直径的半圆长,乙所走的路径长为以AC、CD和DB为直径的三个半圆长的和,然后根据圆的周长公式分别计算他们所走的路径,再比较大小即可.
解答:解:(1)BC=AB-AC=10,
甲所走的路径长=
•2•π•
=
•2•π•
=20π(m),
乙所走的路径长=
•2•π•
+
•2•π•
=
•2•π•
+
•π•
=20π(m),
所以两人所走路程的相等;
(2)两人走的路程远近相同.理由如下:甲所走的路径长=
•2•π•
=
π•AB,
乙所走的路径长=
•2•π•
+
•2•π•
+
•π•
=
π(AC+CD+DB)=
π•AB,
即两人走的路程远近相同.
甲所走的路径长=
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
| 40 |
| 2 |
乙所走的路径长=
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 2 |
| 30 |
| 2 |
| 1 |
| 2 |
| 10 |
| 2 |
所以两人所走路程的相等;
(2)两人走的路程远近相同.理由如下:甲所走的路径长=
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
乙所走的路径长=
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 2 |
| CD |
| 2 |
| 1 |
| 2 |
| BD |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即两人走的路程远近相同.
点评:本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).记住圆的周长公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8,
如图,在矩形ABCD中,E是AD边上的一点,CE交对角线于点O,△DOE面积为2,△COD面积为8, 已知:如图,在△ABC中,BC=2,∠A=45°,∠B=60°,求AC的长.
已知:如图,在△ABC中,BC=2,∠A=45°,∠B=60°,求AC的长.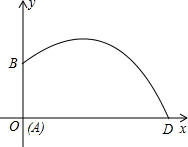 如图,某喷灌设备的喷头B高出地面1.2m,如果喷出的抛物线形水流的水平距离x(m)与高度y(m)之间关系为y=a(x-4)2+2,求水流落地点D与喷头底部A的距离(精确到0.1m)
如图,某喷灌设备的喷头B高出地面1.2m,如果喷出的抛物线形水流的水平距离x(m)与高度y(m)之间关系为y=a(x-4)2+2,求水流落地点D与喷头底部A的距离(精确到0.1m)