题目内容
19.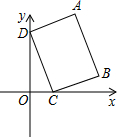 如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )| A. | (2,4) | B. | ($\frac{5}{2}$,4) | C. | (3,4) | D. | (2,5) |
分析 如图,作BM⊥x轴垂足为M,作AH⊥DH垂足为H,构建全等三角形△AHD≌△BCM,结合全等三角形的性质得到DH=CM=2,AH=BM=1,易求点A的坐标.
解答  解:如图,作BM⊥x轴垂足为M,作AH⊥DH垂足为H,
解:如图,作BM⊥x轴垂足为M,作AH⊥DH垂足为H,
∵D的坐标是(0,3),线段AB=$\sqrt{10}$,
∴AB=CD=$\sqrt{10}$,OD=3,
∴OC=1.
又∵B的坐标是(3,1),
∴CM=2,BM=1.易证△AHD≌△BCM,
∴DH=CM=2,AH=BM=1,
∴A(2,4)
故选:A.
点评 本题考查了矩形的性质,坐标与图形性质,做题时,注意题中辅助线的作法.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
9.抛物线y=2x2向右平移1个单位,再向上平移5个单位,则平移后的抛物线的解析式为( )
| A. | y=2(x+1)2+5 | B. | y=2(x+1)2-5 | C. | y=2(x-1)2-5 | D. | y=2(x-1)2+5 |
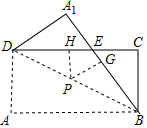 如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4.
如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4. 实数a、b在数轴上的位置如图所示,化简:|a|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=-b.
实数a、b在数轴上的位置如图所示,化简:|a|-$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$=-b.