题目内容
3.如图1,一动点P从点O出发,沿着y=2x以$\sqrt{5}$个单位/秒的速度向点C运动,到点C后,沿着直线AB方向向点B运动.运动速度不变.运动到点B后停止运动,作PE⊥x轴于E,PF⊥y轴于点F.四边形FOEP与△OCB的重叠面积为S(平方单位).运动时间为t(秒)则S与t的函数图象如图2所示.(1)求C点坐标;
(2)求S与t的函数关系式.
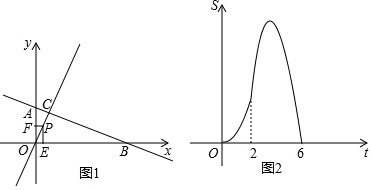
分析 (1)设C(a,2a),a>0,由图2可知OC=2$\sqrt{5}$,根据勾股定理即可求得;
(2)分两种情况考虑:当P在线段OC上,如答题图1所示,矩形与三角形重叠部分为三角形OPE,求出三角形OPE面积即可得到结果;当P在线段BC上,如答题图2所示,重叠部分面积为矩形面积减去三角形OFN面积,列出S关于t的解析式即可.
解答 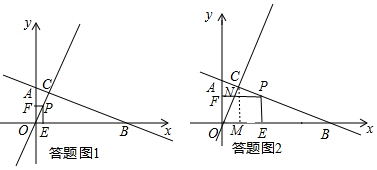 解:(1)∵点C在直线y=2x上,
解:(1)∵点C在直线y=2x上,
∴设C(a,2a),a>0,
由图2可知动点P从点O出发,沿着y=2x以$\sqrt{5}$个单位/秒的速度向点C运动,2秒到点C,
∴OC=2$\sqrt{5}$,
∴a2+(2a)2=(2$\sqrt{5}$)2,
解得a=2,
∴C(2,4);
(2)分两种情况考虑:
当P在线段OC上时,如答题图1所示,根据题意得:OP=$\sqrt{5}$t,
∴P(t,2t),
∴S=S△OPE=$\frac{1}{2}$OE•PE=$\frac{1}{2}$t•2t=t2(0≤t≤2);
当P在线段BC上时,如答题图2所示,根据题意得:BC=4$\sqrt{5}$,
∴CP=(t-2)$\sqrt{5}$,BP=(6-t)$\sqrt{5}$,BM=$\sqrt{B{C}^{2}-C{M}^{2}}$=$\sqrt{(4\sqrt{5})^{2}-{4}^{2}}$=8,
过C作CM⊥x轴,交x轴于点M,设PF与直线y=2x的交点为N,
∵PE∥CM,
∴$\frac{PE}{CM}$=$\frac{PB}{BC}$=$\frac{BE}{BM}$,即$\frac{PE}{4}$=$\frac{(6-t)\sqrt{5}}{4\sqrt{5}}$=$\frac{BE}{8}$,
∴PE=6-t,BE=12-2t,
∵OB=OM+BM=2+8=10,
∴OE=10-(12-2t)=2t-2,
把y=6-t代入y=2x,解得x=3-$\frac{1}{2}$t,
∴PF与直线y=2x的交点横坐标为3-$\frac{1}{2}$t,
∴S=S矩形PEOF-S△OFN=OE•PE-$\frac{1}{2}$FN•OF=(2t-2)•(6-t)-$\frac{1}{2}$(3-$\frac{1}{2}$t)•(6-t)
=-$\frac{9}{4}$t2+17t-21(2<t≤6).
点评 此题属于一次函数综合题,涉及的知识有:一次函数图象上点的坐标特征,勾股定理,以及平行线分线段成比例定理,利用了分类讨论的思想是解本题第二问的关键.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案 如图,AB∥CD,DF⊥EF于F,∠FEB=60°,则∠D的度数是( )
如图,AB∥CD,DF⊥EF于F,∠FEB=60°,则∠D的度数是( )| A. | 80° | B. | 60° | C. | 45° | D. | 30° |
| A. | π | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 0.1010010001 | D. | $\sqrt{2}$ |
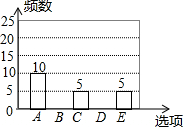 随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):
随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):| 选项 | 频数 | 百分比 |
| A | 10 | m |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | p | 0.4 |
| E | 5 | 0.1 |
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图;
(3)若该中学约有2400名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.

 如图,C、D为线段AB上的两点,M是AC的中点,N是BD的中点.如果MN=a,CD=b,求线段AB的长(用a、b的代数式表示).
如图,C、D为线段AB上的两点,M是AC的中点,N是BD的中点.如果MN=a,CD=b,求线段AB的长(用a、b的代数式表示).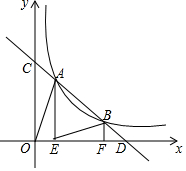 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上(点A在点B的左侧),直线AB分别交x轴,y轴于点D,C,AE⊥x轴于点E,BF⊥x轴于点F,连结AO,BE,已知AB=2BD,△AOC与△BDF的面积之和是△ABE的面积的k倍,则k的值是$\frac{5}{6}$.
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上(点A在点B的左侧),直线AB分别交x轴,y轴于点D,C,AE⊥x轴于点E,BF⊥x轴于点F,连结AO,BE,已知AB=2BD,△AOC与△BDF的面积之和是△ABE的面积的k倍,则k的值是$\frac{5}{6}$.