题目内容
在△ABC中,AB=AC=5,BC=6,求sinA,sinB.
考点:解直角三角形
专题:
分析:过A作AD⊥BC于D,过B作BE⊥AC于E,根据等腰三角形性质求出BD,根据勾股定理求出AD,根据三角形的面积求出BE,解直角三角形求出即可.
解答:解: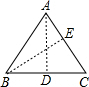
过A作AD⊥BC于D,过B作BE⊥AC于E,
则∠BDA=∠CDA=90°,
∵AB=AC=5,BC=6,
∴BD=DC=3,
由勾股定理得:AD=
=4,
∴△ABC的面积S=
×BC×AD=
AC×BE,
∴6×4=5BE,
∴BE=
,
∴sinA=
=
sinB=
=
.

过A作AD⊥BC于D,过B作BE⊥AC于E,
则∠BDA=∠CDA=90°,
∵AB=AC=5,BC=6,
∴BD=DC=3,
由勾股定理得:AD=
| 52-32 |
∴△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
∴6×4=5BE,
∴BE=
| 24 |
| 5 |
∴sinA=
| BE |
| AB |
| 24 |
| 25 |
sinB=
| AD |
| AB |
| 4 |
| 5 |
点评:本题考查了解直角三角形,等腰三角形的性质,勾股定理的应用,解此题的关键是构造直角三角形,主要考查学生的计算能力.

练习册系列答案
相关题目
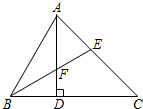 如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )
如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )| A、2个 | B、3个 | C、4个 | D、5个 |
下列方程中,属于一元一次方程的是( )
A、
| ||
| B、2x+y=6 | ||
| C、3x=1 | ||
| D、x2-1=3 |
解是x=1的一元一次方程是( )
| A、1-x=2 | ||
| B、-x=1 | ||
| C、2x-3=-1 | ||
D、
|
 如图,直角三角形ABC的斜边AB在直线l上,把△ABC按顺时针方向在l上转动两次,使它转到△A′B′C′的位置,设BC=1,AC=
如图,直角三角形ABC的斜边AB在直线l上,把△ABC按顺时针方向在l上转动两次,使它转到△A′B′C′的位置,设BC=1,AC=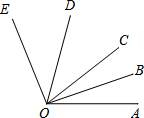 如图,OB是∠AOC的平分线,OD是∠EOC的平分线.
如图,OB是∠AOC的平分线,OD是∠EOC的平分线.