题目内容
3.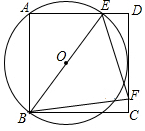 如图,正方形ABCD的边长为2,点E在边AD上(不与A,D重合),点F在边CD上,且∠EBF=45°,若△ABE的外接圆⊙O与CD边相切.
如图,正方形ABCD的边长为2,点E在边AD上(不与A,D重合),点F在边CD上,且∠EBF=45°,若△ABE的外接圆⊙O与CD边相切.(1)求⊙O的半径长;
(2)求△BEF的面积.
分析 (1)将△BCF绕点B逆时针旋转90°到△BAP,过点B作BQ⊥EF,设⊙O与CD相切于点M,连接OM,延长MO交AB于点N,由已知得出△BPE≌△BFE,进而得出△AEB≌△QEB,利用中位线出AE的长,由勾股定理求出BE,即可得出半径;
(2)由C△EFD=4,利用勾股定理得出DF的长,即可求出△BEF的面积.
解答 解:(1)将△BCF绕点B逆时针旋转90°到△BAP,过点B作BQ⊥EF,设⊙O与CD相切于点M,连接OM,延长MO交AB于点N,如图所示: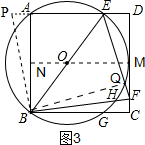
在△BPE与△BFE中,$\left\{\begin{array}{l}{BP=BF}&{\;}\\{∠PBE=∠EBF}&{\;}\\{BE=BE}&{\;}\end{array}\right.$,
∴△BPE≌△BFE(SAS),
∴∠AEB=∠BEQ,PE=EF,
在△AEB和△QEB中,$\left\{\begin{array}{l}{∠BAE=∠BQE}&{\;}\\{∠AEB=∠BEQ}&{\;}\\{BE=BE}&{\;}\end{array}\right.$,
∴△AEB≌△QEB(AAS),
∴BQ=AB=2,
由PE=EF可知,
C△EFD=ED+DF+EF=ED+DF+PE=ED+DF+PA+AE=ED+AE+DF+FC=4,
设AE=a,则DE=2-a,BE=$\sqrt{4+{a}^{2}}$,
∵O为BE中点,且MN∥AD,
∴ON=$\frac{1}{2}$AE=$\frac{a}{2}$,
∴OM=2-$\frac{a}{2}$,
又BE=2OM,
∴$\sqrt{4+{a}^{2}}$=4-a,解得a=$\frac{3}{2}$,
∴ED=$\frac{1}{2}$,BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\frac{5}{2}$,
∴⊙O的半径长=$\frac{1}{2}$BE=$\frac{5}{4}$;
(2)∵C△EFD=4,设DF=b,
∴EF=4-b-$\frac{1}{2}$=$\frac{7}{2}$-b,
在Rt△EDF中,($\frac{1}{2}$)2+b2=($\frac{7}{2}$-b)2,
解得b=$\frac{12}{7}$,
∴EF=$\frac{7}{2}$-$\frac{12}{7}$=$\frac{25}{14}$,
∴S△BEF=$\frac{1}{2}$×$\frac{25}{14}$×2=$\frac{25}{14}$.
点评 本题主要考查了切线的性质、勾股定理、全等三角形的判定与性质等知识;本题综合性强,解题的关键是正确作出辅助线,利用三解形全等及方程灵活的求解.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | 4 | B. | 2 | C. | 0 | D. | -4 |
| A. | m3+m2=m5 | B. | m5÷m2=m3 | C. | (2m)3=6m3 | D. | (m+1)2=m2+1 |
| A. | x<z<y | B. | x<y<z | C. | y<z<x | D. | z<y<x |
| A. | x<-1 | B. | x≥3 | C. | -1<x≤3 | D. | 无解 |
| A. | 一、三象限 | B. | 二、四象限 | C. | 一、二象限 | D. | 三、四象限 |
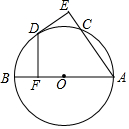 如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC的延长线于E,DF⊥AB于F.
如图,AB为⊙O直径,C为⊙O上一点,点D是$\widehat{BC}$的中点,过D作⊙O的切线交AC的延长线于E,DF⊥AB于F.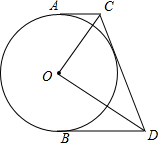 如图,已知AC,BD与⊙O相切于点A,B,且AC∥BD,若∠COD=90°,求证:CD是⊙O的切线.
如图,已知AC,BD与⊙O相切于点A,B,且AC∥BD,若∠COD=90°,求证:CD是⊙O的切线.