题目内容

若抛物线y=ax2+bx+c经过点A（1，6）、B（-5，6），则该抛物线的对称轴为
 
．
考点：二次函数的性质
专题：
分析：根据经过的两点的纵坐标相等可得两点关于对称轴对称，然后列式求解即可得到对称轴解析式．
解答：解：∵抛物线y=ax2+bx+c经过点A（1，6）、B（-5，6），
∴对称轴为直线x=
1-5
2
=-2．
故答案为：直线x=-2．
点评：本题考查了二次函数的性质，根据纵坐标判断出两点关于对称轴对称是解题的关键．
练习册系列答案
相关题目
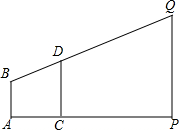如图所示，旗杆顶部Q，标杆顶部D，观测者的眼睛B在同一直线上，测得观测者的脚到旗杆底部的距离AP=75m，观测者的脚到标杆底部的距离AC=2.5m，若AB=1.5m，标杆CD的高为2m，那么旗杆有多高．
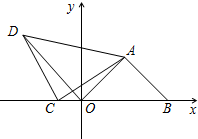如图，在平面直角坐标系中，△AOB为等腰直角三角形，AB=OA，B（8，0），C为x轴负半轴上一动点，以AC为直角边作等腰直角△ACD，∠ACD=90°，连OD．
（1）A点的坐标为
 
；
（2）作CH⊥x轴交AO的延长线于点H，
①求证：△DCO≌△ACH；
②求∠AOD的度数；
（3）当点C在线段OB（不含端点）上运动时，∠AOD的度数是否发生变化？请说明你的理由．
已知b+
1
c
=1，c+
1
a
=1，求证：a+
1
b
=1．
解关于x的方程：
b+x
a
+2=
x-a
b
（a≠b）．
数轴上一个点到原点距离为5，那么这个点表示的数为
 
．
115°÷4=
 
．
如图，已知线段AB的两个端点在直角坐标系中的坐标分别是A（m，m），B（2n，n），以原点O为位似中心，相似比为
1
2
，把线段AB缩小，则经过位似变换后A、B的对应点坐标分别是A′
 
，B′
 
；点A到原点O的距离是
 
．
如图，为估计池塘岸边A，B两点间的距离，在池塘的一侧选取点O，分别取OA，OB 的中点M，N，测得MN=32m，则A，B两点间的距离是（　　）
A、64mB、16m
C、32mD、24m

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网